Abstand Punkt Ebene
About points...
We associate a certain number of points with each exercise.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
About difficulty...
We associate a certain difficulty with each exercise.
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
Question
Solution
Short
Video
\(\LaTeX\)
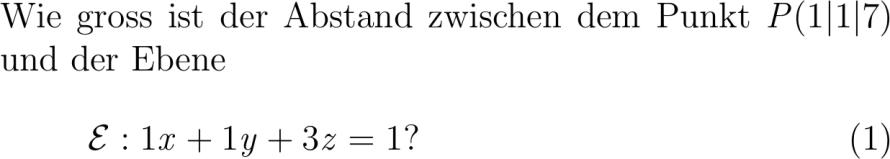

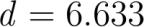
No explanation / solution video to this exercise has yet been created.
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Exercise:
Wie gross ist der Abstand zwischen dem Punkt PPxX|PyX|PzX und der Ebene mathcalE: Ex x +Ey y +Ez z Eih?
Solution:
tdplotsetmaincoords center tikzpicturelatex scale. tdplot_main_coords tikzsetscaled unit vectors. filldrawcolorblack fillyellow!!white opacity. scaled cs -------.---.--cycle; foreach x in --... drawcolorgray scaled cs x---x; foreach y in --... drawcolorgray scaled cs -y--y; drawcolorgreen!!black- scaled cs --- noderight small bmx; drawcolorgreen!!black- scaled cs --- nodeabove small bmy; drawcolorgreen!!black- scaled cs --- nodeleft small bmz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillred!!yellow coordinatesPxXPyXPzX noderightred!!yellow tiny PPx|Py|Pz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblue coordinatesFxXFyXFzX noderightblue tiny FFxX|FyX|FzX; draw- stealth colorred thick scaled cs PxXPyXPzX--FxXFyXFzX nodemidway right tiny vec d; tikzpicture center bf . Lösungsweg Lotfusspunktverfahren Zunächst muss der Normalenvektor der Ebene mathcalE gefunden bzw. abgelesen werden: mathcalE: Ex x +Ey y +Ez z Eih vec n pmatrix Ex Ey Ez pmatrix Anschliess wird die Lotgerade welche senkrecht zur Ebene steht und durch S verläuft ermittelt: ell:vec X vec S + lambda vec n hspace.cm; lambda in mathbbR ell:vec X pmatrix Px Py Pz pmatrix + lambda pmatrix Ex Ey Ez pmatrix hspace.cm; lambda in mathbbR Durch Schneiden dieser Lotgerade mit der Ebene erhält man den Lotfusspunkt: Ex Px + Ex lambda + Ey Py + Ey lambda + Ez Pz + Ez lambda ZX + LX lambda LX lambda -ZX lambda -lX lambda kann nun in die Gleichung eingesetzt werden wodurch man die Koordinaten des Lotfusspunktes ermittelt: ell:vec X pmatrix Px Py Pz pmatrix - lX pmatrix Ex Ey Ez pmatrix hspace.cm; lambda in mathbbR F FxX|FyX|FzX Nun muss man nur noch den Abstand zwischen P und F bestimmen: vec d vec s_ - vec r_ pmatrix x_F y_F z_F pmatrix - pmatrix x_P y_P z_P pmatrix pmatrix FxX FyX FzX pmatrix - pmatrix PxX PyX PzX pmatrix pmatrix DX EX FX pmatrix |vec d| sqrtx_F-x_P^+y_F-y_P^+z_F-z_P^ sqrtFxX-PxX^+FyX-PyX^+FzX-PzX^ sqrtDX^+EX^+FX^ G bf . Lösungsweg Hessesche Normalform Hierbei setzt man die Werte der Aufgabe einfach in die folge Lösungsformel ein: d left |fracax+by+cz+dsqrt a^+b^+c^ right | d left |fracEx x+Ey y+Ez z+Eihsqrt Ex^+Ey^+Ez^ right | fracZXsqrt LX G
Wie gross ist der Abstand zwischen dem Punkt PPxX|PyX|PzX und der Ebene mathcalE: Ex x +Ey y +Ez z Eih?
Solution:
tdplotsetmaincoords center tikzpicturelatex scale. tdplot_main_coords tikzsetscaled unit vectors. filldrawcolorblack fillyellow!!white opacity. scaled cs -------.---.--cycle; foreach x in --... drawcolorgray scaled cs x---x; foreach y in --... drawcolorgray scaled cs -y--y; drawcolorgreen!!black- scaled cs --- noderight small bmx; drawcolorgreen!!black- scaled cs --- nodeabove small bmy; drawcolorgreen!!black- scaled cs --- nodeleft small bmz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillred!!yellow coordinatesPxXPyXPzX noderightred!!yellow tiny PPx|Py|Pz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblue coordinatesFxXFyXFzX noderightblue tiny FFxX|FyX|FzX; draw- stealth colorred thick scaled cs PxXPyXPzX--FxXFyXFzX nodemidway right tiny vec d; tikzpicture center bf . Lösungsweg Lotfusspunktverfahren Zunächst muss der Normalenvektor der Ebene mathcalE gefunden bzw. abgelesen werden: mathcalE: Ex x +Ey y +Ez z Eih vec n pmatrix Ex Ey Ez pmatrix Anschliess wird die Lotgerade welche senkrecht zur Ebene steht und durch S verläuft ermittelt: ell:vec X vec S + lambda vec n hspace.cm; lambda in mathbbR ell:vec X pmatrix Px Py Pz pmatrix + lambda pmatrix Ex Ey Ez pmatrix hspace.cm; lambda in mathbbR Durch Schneiden dieser Lotgerade mit der Ebene erhält man den Lotfusspunkt: Ex Px + Ex lambda + Ey Py + Ey lambda + Ez Pz + Ez lambda ZX + LX lambda LX lambda -ZX lambda -lX lambda kann nun in die Gleichung eingesetzt werden wodurch man die Koordinaten des Lotfusspunktes ermittelt: ell:vec X pmatrix Px Py Pz pmatrix - lX pmatrix Ex Ey Ez pmatrix hspace.cm; lambda in mathbbR F FxX|FyX|FzX Nun muss man nur noch den Abstand zwischen P und F bestimmen: vec d vec s_ - vec r_ pmatrix x_F y_F z_F pmatrix - pmatrix x_P y_P z_P pmatrix pmatrix FxX FyX FzX pmatrix - pmatrix PxX PyX PzX pmatrix pmatrix DX EX FX pmatrix |vec d| sqrtx_F-x_P^+y_F-y_P^+z_F-z_P^ sqrtFxX-PxX^+FyX-PyX^+FzX-PzX^ sqrtDX^+EX^+FX^ G bf . Lösungsweg Hessesche Normalform Hierbei setzt man die Werte der Aufgabe einfach in die folge Lösungsformel ein: d left |fracax+by+cz+dsqrt a^+b^+c^ right | d left |fracEx x+Ey y+Ez z+Eihsqrt Ex^+Ey^+Ez^ right | fracZXsqrt LX G
Meta Information
Exercise:
Wie gross ist der Abstand zwischen dem Punkt PPxX|PyX|PzX und der Ebene mathcalE: Ex x +Ey y +Ez z Eih?
Solution:
tdplotsetmaincoords center tikzpicturelatex scale. tdplot_main_coords tikzsetscaled unit vectors. filldrawcolorblack fillyellow!!white opacity. scaled cs -------.---.--cycle; foreach x in --... drawcolorgray scaled cs x---x; foreach y in --... drawcolorgray scaled cs -y--y; drawcolorgreen!!black- scaled cs --- noderight small bmx; drawcolorgreen!!black- scaled cs --- nodeabove small bmy; drawcolorgreen!!black- scaled cs --- nodeleft small bmz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillred!!yellow coordinatesPxXPyXPzX noderightred!!yellow tiny PPx|Py|Pz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblue coordinatesFxXFyXFzX noderightblue tiny FFxX|FyX|FzX; draw- stealth colorred thick scaled cs PxXPyXPzX--FxXFyXFzX nodemidway right tiny vec d; tikzpicture center bf . Lösungsweg Lotfusspunktverfahren Zunächst muss der Normalenvektor der Ebene mathcalE gefunden bzw. abgelesen werden: mathcalE: Ex x +Ey y +Ez z Eih vec n pmatrix Ex Ey Ez pmatrix Anschliess wird die Lotgerade welche senkrecht zur Ebene steht und durch S verläuft ermittelt: ell:vec X vec S + lambda vec n hspace.cm; lambda in mathbbR ell:vec X pmatrix Px Py Pz pmatrix + lambda pmatrix Ex Ey Ez pmatrix hspace.cm; lambda in mathbbR Durch Schneiden dieser Lotgerade mit der Ebene erhält man den Lotfusspunkt: Ex Px + Ex lambda + Ey Py + Ey lambda + Ez Pz + Ez lambda ZX + LX lambda LX lambda -ZX lambda -lX lambda kann nun in die Gleichung eingesetzt werden wodurch man die Koordinaten des Lotfusspunktes ermittelt: ell:vec X pmatrix Px Py Pz pmatrix - lX pmatrix Ex Ey Ez pmatrix hspace.cm; lambda in mathbbR F FxX|FyX|FzX Nun muss man nur noch den Abstand zwischen P und F bestimmen: vec d vec s_ - vec r_ pmatrix x_F y_F z_F pmatrix - pmatrix x_P y_P z_P pmatrix pmatrix FxX FyX FzX pmatrix - pmatrix PxX PyX PzX pmatrix pmatrix DX EX FX pmatrix |vec d| sqrtx_F-x_P^+y_F-y_P^+z_F-z_P^ sqrtFxX-PxX^+FyX-PyX^+FzX-PzX^ sqrtDX^+EX^+FX^ G bf . Lösungsweg Hessesche Normalform Hierbei setzt man die Werte der Aufgabe einfach in die folge Lösungsformel ein: d left |fracax+by+cz+dsqrt a^+b^+c^ right | d left |fracEx x+Ey y+Ez z+Eihsqrt Ex^+Ey^+Ez^ right | fracZXsqrt LX G
Wie gross ist der Abstand zwischen dem Punkt PPxX|PyX|PzX und der Ebene mathcalE: Ex x +Ey y +Ez z Eih?
Solution:
tdplotsetmaincoords center tikzpicturelatex scale. tdplot_main_coords tikzsetscaled unit vectors. filldrawcolorblack fillyellow!!white opacity. scaled cs -------.---.--cycle; foreach x in --... drawcolorgray scaled cs x---x; foreach y in --... drawcolorgray scaled cs -y--y; drawcolorgreen!!black- scaled cs --- noderight small bmx; drawcolorgreen!!black- scaled cs --- nodeabove small bmy; drawcolorgreen!!black- scaled cs --- nodeleft small bmz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillred!!yellow coordinatesPxXPyXPzX noderightred!!yellow tiny PPx|Py|Pz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblue coordinatesFxXFyXFzX noderightblue tiny FFxX|FyX|FzX; draw- stealth colorred thick scaled cs PxXPyXPzX--FxXFyXFzX nodemidway right tiny vec d; tikzpicture center bf . Lösungsweg Lotfusspunktverfahren Zunächst muss der Normalenvektor der Ebene mathcalE gefunden bzw. abgelesen werden: mathcalE: Ex x +Ey y +Ez z Eih vec n pmatrix Ex Ey Ez pmatrix Anschliess wird die Lotgerade welche senkrecht zur Ebene steht und durch S verläuft ermittelt: ell:vec X vec S + lambda vec n hspace.cm; lambda in mathbbR ell:vec X pmatrix Px Py Pz pmatrix + lambda pmatrix Ex Ey Ez pmatrix hspace.cm; lambda in mathbbR Durch Schneiden dieser Lotgerade mit der Ebene erhält man den Lotfusspunkt: Ex Px + Ex lambda + Ey Py + Ey lambda + Ez Pz + Ez lambda ZX + LX lambda LX lambda -ZX lambda -lX lambda kann nun in die Gleichung eingesetzt werden wodurch man die Koordinaten des Lotfusspunktes ermittelt: ell:vec X pmatrix Px Py Pz pmatrix - lX pmatrix Ex Ey Ez pmatrix hspace.cm; lambda in mathbbR F FxX|FyX|FzX Nun muss man nur noch den Abstand zwischen P und F bestimmen: vec d vec s_ - vec r_ pmatrix x_F y_F z_F pmatrix - pmatrix x_P y_P z_P pmatrix pmatrix FxX FyX FzX pmatrix - pmatrix PxX PyX PzX pmatrix pmatrix DX EX FX pmatrix |vec d| sqrtx_F-x_P^+y_F-y_P^+z_F-z_P^ sqrtFxX-PxX^+FyX-PyX^+FzX-PzX^ sqrtDX^+EX^+FX^ G bf . Lösungsweg Hessesche Normalform Hierbei setzt man die Werte der Aufgabe einfach in die folge Lösungsformel ein: d left |fracax+by+cz+dsqrt a^+b^+c^ right | d left |fracEx x+Ey y+Ez z+Eihsqrt Ex^+Ey^+Ez^ right | fracZXsqrt LX G
Contained in these collections:

