Abstand von Punkt zu Gerade
About points...
We associate a certain number of points with each exercise.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
About difficulty...
We associate a certain difficulty with each exercise.
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
Question
Solution
Short
Video
\(\LaTeX\)
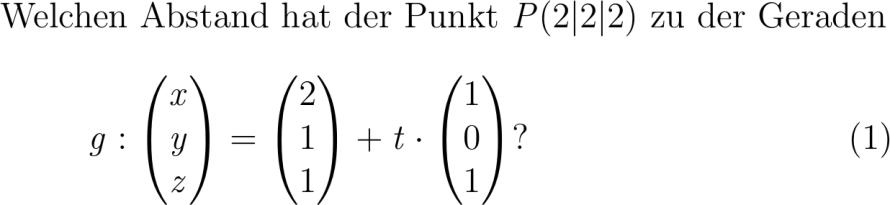

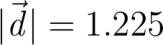
No explanation / solution video to this exercise has yet been created.
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Exercise:
Welchen Abstand hat der Punkt PPx|Py|Pz zu der Geraden g: pmatrix x y z pmatrix pmatrix gx gy gz pmatrix + t pmatrix tx ty tz pmatrix?
Solution:
tikzset glow/.style preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. bf . Berechnungsmethode tdplotsetmaincoords center tikzpicturelatex scale. tdplot_main_coords tikzsetscaled unit vectors. foreach x in -... drawcolorgray scaled cs x---x; foreach y in -... drawcolorgray scaled cs -y--y; drawcolorgreen!!black- scaled cs ---. noderight small bmx; drawcolorgreen!!black- scaled cs ---. nodeabove small bmy; drawcolorgreen!!black- scaled cs --- nodeleft small bmz; drawdotted scaled cs LxX LyX LzX--LxX LyX ; drawdotted scaled cs PxX PyX PzX--PxX PyX ; drawdotted scaled cs gxX gyX gzX--gxX gyX ; drawcolorblue scaled cs gxXgyXgzX--+-*txX-*tyX-*tzX nodeleftsmallg; drawcolorblue scaled cs gxXgyXgzX--+*txX*tyX*tzX; draw- stealth colorred thick scaled cs gxXgyXgzX--+txXtyXtzX nodeleft tiny pmatrix tx ty tzpmatrix vec v; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblue!!white coordinatesgxXgyXgzX noderight tiny Dgx|gy|gz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillviolet!!white coordinatesLxXLyXLzX nodeleftred!!blue tiny L; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillred!!yellow coordinatesPxXPyXPzX noderight red!!yellow tiny PPx|Py|Pz; draw- stealth colorred!!yellow thick dashed scaled cs --+PxXPyXPzX nodemidway above tiny vec r_P; draw- stealth colorred!!blue thick dashed scaled cs --+LxXLyXLzX nodemidway left tiny vec r_L; draw- stealth colorolive thick scaled cs PxXPyXPzX--LxX LyX LzX nodemidway above tiny vec d; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesLxXLyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesgxXgyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesPxXPyX; tikzpicture center Um den Abstand zu berechnen muss als erstes der Lotfusspunkt L auf der Geraden g gefunden werden. Weil der Vektor vecPL rechtwinklig zum Vektor vec v in Richtung der Geraden sein muss deren Skalarprodukt also verschwinden muss gilt: leftvec L - vec Pright vec v &mustbe leftpmatrix L_x L_y L_zpmatrix - pmatrix Px Py Pz pmatrix right pmatrix tx ty tz pmatrix &mustbe Der Punkt L ist unbekannt aber liegt auf der Geraden weshalb man schreiben kann: leftpmatrix gx - t tx gy - t ty gz - t tzpmatrix - pmatrix Px Py Pz pmatrix right pmatrix tx ty tz pmatrix &mustbe pmatrix - t tx - - t ty - - t tzpmatrix pmatrix tx ty tz pmatrix &mustbe Skalarprodukt ausrechnen und auflösen nach t liefert: t . Damit findet man den Lotfusspunkt: pmatrix L_x L_y L_zpmatrix pmatrix gx gy gz pmatrix + . pmatrix tx ty tz pmatrix pmatrix Lx Ly Lz pmatrix Der Abstand zwischen den Punkten L und P kann nun leicht berechnet werden: vec d vec r_L - vec r_P pmatrix x_L y_L z_L pmatrix - pmatrix x_P y_P z_P pmatrix pmatrix LxX LyX LzX pmatrix - pmatrix PxX PyX PzX pmatrix pmatrix AX BX CX pmatrix |vec d| sqrtx_L-x_P^+y_L-y_P^+z_L-z_P^ sqrtLxX-PxX^+LyX-PyX^+LzX-PzX^ sqrtAX^+BX^+CX^ G bf . Berechnungsmethode tdplotsetmaincoords center tikzpicturelatex scale. tdplot_main_coords tikzsetscaled unit vectors. foreach x in -... drawcolorgray scaled cs x---x; foreach y in -... drawcolorgray scaled cs -y--y; drawcolorgreen!!black- scaled cs ---. noderight small bmx; drawcolorgreen!!black- scaled cs ---. nodeabove small bmy; drawcolorgreen!!black- scaled cs --- nodeleft small bmz; drawdotted scaled cs PxX PyX PzX--PxX PyX ; drawdotted scaled cs gxX gyX gzX--gxX gyX ; drawcolorblue scaled cs gxXgyXgzX--+-*txX-*tyX-*tzX nodeleftsmallg; drawcolorblue scaled cs gxXgyXgzX--+*txX*tyX*tzX; draw- stealth colorred thick scaled cs gxXgyXgzX--+txXtyXtzX nodemidwayleft tiny vec v; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblue!!white coordinatesgxX+txXgyX+tyXgzX+tzX nodeleft tiny BBxX|ByX|BzX; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblue!!white coordinatesgxXgyXgzX noderight tiny Agx|gy|gz; draw- stealth colorred!!white dashed thick scaled cs glowred PxXPyXPzX--+txXtyXtzX nodemidway right tiny vec v; draw- stealth colororange!!white dashed thick scaled cs glowyellow gxXgyXgzX--PxXPyXPzX nodemidway below tiny vec AP; draw- stealth colorred!!white dashed thick scaled cs glowyellow BxXByXBzX--+sxXsyXszX; filldrawcolorblack fillyellow!!white opacity. scaled csgxXgyXgzX--BxXByXBzX--QxXQyXQzX--PxXPyXPzX--cycle; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillred!!yellow coordinatesPxXPyXPzX noderight red!!yellow tiny PPx|Py|Pz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblack coordinatesQxXQyXQzX noderight tiny QQxX|QyX|QzX; draw- stealth colorolive thick scaled cs PxXPyXPzX--LxX LyX LzX nodemidway above tiny vec d; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesLxXLyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesgxXgyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesPxXPyX; tikzpicture center Die Fläche des von AB und P aufgespannten Parallelogramms lässt sich darstellen als: F_APQB overlineAB |vec d| Diese Gleichung kann man mithilfe des Kreuzprodukts umformulieren in: F_APQB |vecABtimes vecAP| |vec d| d fracF_APQBoverlineAB d frac|vecABtimes vecAP|overlineAB In diese Formel können nun die konkreten Werte der Aufgabe eingesetzt werden: d fracleft|pmatrix bxX byX bzX pmatrix times pmatrix pxX pyX pzX pmatrixright| overlinepmatrix bxX byX bzX pmatrix fracleft|pmatrix kxX kyX kzX pmatrixright|overlinepmatrix bxX byX bzX pmatrix fracDE F bf . Berechnungsmethode tdplotsetmaincoords center tikzpicturelatex scale. tdplot_main_coords tikzsetscaled unit vectors. foreach x in -... drawcolorgray scaled cs x---x; foreach y in -... drawcolorgray scaled cs -y--y; drawcolorgreen!!black- scaled cs ---. noderight small bmx; drawcolorgreen!!black- scaled cs ---. nodeabove small bmy; drawcolorgreen!!black- scaled cs --- nodeleft small bmz; drawdotted scaled cs LxX LyX LzX--LxX LyX ; drawdotted scaled cs PxX PyX PzX--PxX PyX ; drawdotted scaled cs gxX gyX gzX--gxX gyX ; drawcolorblue scaled cs gxXgyXgzX--+-*txX-*tyX-*tzX nodeleftsmallg; drawcolorblue scaled cs gxXgyXgzX--+*txX*tyX*tzX; drawcoloryellow!!red very thick scaled cs glowyellow --.. nodebelowsmallmathcalE; draw- stealth colorred thick scaled cs gxXgyXgzX--+txXtyXtzX nodeleft tiny pmatrix tx ty tzpmatrix vec v; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblue!!white coordinatesgxXgyXgzX noderight tiny Dgx|gy|gz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillviolet!!white coordinatesLxXLyXLzX nodeleftred!!blue tiny SLx|Ly|Lz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillred!!yellow coordinatesPxXPyXPzX noderight red!!yellow tiny PPx|Py|Pz; draw- stealth colorred!!yellow thick dashed scaled cs --+PxXPyXPzX nodemidway above tiny vec r_P; draw- stealth colorolive thick scaled cs PxXPyXPzX--LxX LyX LzX nodemidway above tiny vec d; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesLxXLyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesgxXgyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesPxXPyX; tikzpicture center Normalenvektor von g ablesen: vec n pmatrix tx ty tz pmatrix tx x + ty y + tz z + D P einsetzen und so D bestimmen: hxX+hyX+hzX + D Rightarrow D HX Daraus folgt dann die Ebenengleichung: tx x + tz z HX Normalebene durch P zu g schneiden mit g dafür werden zunächst die Komponentengleichungen von g aufgestellt: center x gx+tx t y gy+ty t z gz+tz t center Anschliess wird der Schnittpunkt S bestimmt: center tx gx+tx t + tz gz+tz t HX ixX+jxX t + izX+jzX t HX lX+mX t t nX Rightarrow S uxX|uyX|uzX center Vergleicht man diesen S mit dem Lotfusspunkt L aus der ersten Berechungsmethode fällt auf dass es sich bei den beiden um den gleichen Punkt handelt. Nun muss nur noch der Abstand zwischen P und S bestimmt werden: vec d vec r_S - vec r_P pmatrix x_S y_S z_S pmatrix - pmatrix x_P y_P z_P pmatrix pmatrix uxX uyX uzX pmatrix - pmatrix PxX PyX PzX pmatrix pmatrix AX BX CX pmatrix |vec d| sqrtx_S-x_P^+y_S-y_P^+z_S-z_P^ sqrtLxX-PxX^+LyX-PyX^+LzX-PzX^ sqrtAX^+BX^+CX^ G
Welchen Abstand hat der Punkt PPx|Py|Pz zu der Geraden g: pmatrix x y z pmatrix pmatrix gx gy gz pmatrix + t pmatrix tx ty tz pmatrix?
Solution:
tikzset glow/.style preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. bf . Berechnungsmethode tdplotsetmaincoords center tikzpicturelatex scale. tdplot_main_coords tikzsetscaled unit vectors. foreach x in -... drawcolorgray scaled cs x---x; foreach y in -... drawcolorgray scaled cs -y--y; drawcolorgreen!!black- scaled cs ---. noderight small bmx; drawcolorgreen!!black- scaled cs ---. nodeabove small bmy; drawcolorgreen!!black- scaled cs --- nodeleft small bmz; drawdotted scaled cs LxX LyX LzX--LxX LyX ; drawdotted scaled cs PxX PyX PzX--PxX PyX ; drawdotted scaled cs gxX gyX gzX--gxX gyX ; drawcolorblue scaled cs gxXgyXgzX--+-*txX-*tyX-*tzX nodeleftsmallg; drawcolorblue scaled cs gxXgyXgzX--+*txX*tyX*tzX; draw- stealth colorred thick scaled cs gxXgyXgzX--+txXtyXtzX nodeleft tiny pmatrix tx ty tzpmatrix vec v; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblue!!white coordinatesgxXgyXgzX noderight tiny Dgx|gy|gz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillviolet!!white coordinatesLxXLyXLzX nodeleftred!!blue tiny L; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillred!!yellow coordinatesPxXPyXPzX noderight red!!yellow tiny PPx|Py|Pz; draw- stealth colorred!!yellow thick dashed scaled cs --+PxXPyXPzX nodemidway above tiny vec r_P; draw- stealth colorred!!blue thick dashed scaled cs --+LxXLyXLzX nodemidway left tiny vec r_L; draw- stealth colorolive thick scaled cs PxXPyXPzX--LxX LyX LzX nodemidway above tiny vec d; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesLxXLyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesgxXgyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesPxXPyX; tikzpicture center Um den Abstand zu berechnen muss als erstes der Lotfusspunkt L auf der Geraden g gefunden werden. Weil der Vektor vecPL rechtwinklig zum Vektor vec v in Richtung der Geraden sein muss deren Skalarprodukt also verschwinden muss gilt: leftvec L - vec Pright vec v &mustbe leftpmatrix L_x L_y L_zpmatrix - pmatrix Px Py Pz pmatrix right pmatrix tx ty tz pmatrix &mustbe Der Punkt L ist unbekannt aber liegt auf der Geraden weshalb man schreiben kann: leftpmatrix gx - t tx gy - t ty gz - t tzpmatrix - pmatrix Px Py Pz pmatrix right pmatrix tx ty tz pmatrix &mustbe pmatrix - t tx - - t ty - - t tzpmatrix pmatrix tx ty tz pmatrix &mustbe Skalarprodukt ausrechnen und auflösen nach t liefert: t . Damit findet man den Lotfusspunkt: pmatrix L_x L_y L_zpmatrix pmatrix gx gy gz pmatrix + . pmatrix tx ty tz pmatrix pmatrix Lx Ly Lz pmatrix Der Abstand zwischen den Punkten L und P kann nun leicht berechnet werden: vec d vec r_L - vec r_P pmatrix x_L y_L z_L pmatrix - pmatrix x_P y_P z_P pmatrix pmatrix LxX LyX LzX pmatrix - pmatrix PxX PyX PzX pmatrix pmatrix AX BX CX pmatrix |vec d| sqrtx_L-x_P^+y_L-y_P^+z_L-z_P^ sqrtLxX-PxX^+LyX-PyX^+LzX-PzX^ sqrtAX^+BX^+CX^ G bf . Berechnungsmethode tdplotsetmaincoords center tikzpicturelatex scale. tdplot_main_coords tikzsetscaled unit vectors. foreach x in -... drawcolorgray scaled cs x---x; foreach y in -... drawcolorgray scaled cs -y--y; drawcolorgreen!!black- scaled cs ---. noderight small bmx; drawcolorgreen!!black- scaled cs ---. nodeabove small bmy; drawcolorgreen!!black- scaled cs --- nodeleft small bmz; drawdotted scaled cs PxX PyX PzX--PxX PyX ; drawdotted scaled cs gxX gyX gzX--gxX gyX ; drawcolorblue scaled cs gxXgyXgzX--+-*txX-*tyX-*tzX nodeleftsmallg; drawcolorblue scaled cs gxXgyXgzX--+*txX*tyX*tzX; draw- stealth colorred thick scaled cs gxXgyXgzX--+txXtyXtzX nodemidwayleft tiny vec v; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblue!!white coordinatesgxX+txXgyX+tyXgzX+tzX nodeleft tiny BBxX|ByX|BzX; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblue!!white coordinatesgxXgyXgzX noderight tiny Agx|gy|gz; draw- stealth colorred!!white dashed thick scaled cs glowred PxXPyXPzX--+txXtyXtzX nodemidway right tiny vec v; draw- stealth colororange!!white dashed thick scaled cs glowyellow gxXgyXgzX--PxXPyXPzX nodemidway below tiny vec AP; draw- stealth colorred!!white dashed thick scaled cs glowyellow BxXByXBzX--+sxXsyXszX; filldrawcolorblack fillyellow!!white opacity. scaled csgxXgyXgzX--BxXByXBzX--QxXQyXQzX--PxXPyXPzX--cycle; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillred!!yellow coordinatesPxXPyXPzX noderight red!!yellow tiny PPx|Py|Pz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblack coordinatesQxXQyXQzX noderight tiny QQxX|QyX|QzX; draw- stealth colorolive thick scaled cs PxXPyXPzX--LxX LyX LzX nodemidway above tiny vec d; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesLxXLyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesgxXgyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesPxXPyX; tikzpicture center Die Fläche des von AB und P aufgespannten Parallelogramms lässt sich darstellen als: F_APQB overlineAB |vec d| Diese Gleichung kann man mithilfe des Kreuzprodukts umformulieren in: F_APQB |vecABtimes vecAP| |vec d| d fracF_APQBoverlineAB d frac|vecABtimes vecAP|overlineAB In diese Formel können nun die konkreten Werte der Aufgabe eingesetzt werden: d fracleft|pmatrix bxX byX bzX pmatrix times pmatrix pxX pyX pzX pmatrixright| overlinepmatrix bxX byX bzX pmatrix fracleft|pmatrix kxX kyX kzX pmatrixright|overlinepmatrix bxX byX bzX pmatrix fracDE F bf . Berechnungsmethode tdplotsetmaincoords center tikzpicturelatex scale. tdplot_main_coords tikzsetscaled unit vectors. foreach x in -... drawcolorgray scaled cs x---x; foreach y in -... drawcolorgray scaled cs -y--y; drawcolorgreen!!black- scaled cs ---. noderight small bmx; drawcolorgreen!!black- scaled cs ---. nodeabove small bmy; drawcolorgreen!!black- scaled cs --- nodeleft small bmz; drawdotted scaled cs LxX LyX LzX--LxX LyX ; drawdotted scaled cs PxX PyX PzX--PxX PyX ; drawdotted scaled cs gxX gyX gzX--gxX gyX ; drawcolorblue scaled cs gxXgyXgzX--+-*txX-*tyX-*tzX nodeleftsmallg; drawcolorblue scaled cs gxXgyXgzX--+*txX*tyX*tzX; drawcoloryellow!!red very thick scaled cs glowyellow --.. nodebelowsmallmathcalE; draw- stealth colorred thick scaled cs gxXgyXgzX--+txXtyXtzX nodeleft tiny pmatrix tx ty tzpmatrix vec v; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblue!!white coordinatesgxXgyXgzX noderight tiny Dgx|gy|gz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillviolet!!white coordinatesLxXLyXLzX nodeleftred!!blue tiny SLx|Ly|Lz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillred!!yellow coordinatesPxXPyXPzX noderight red!!yellow tiny PPx|Py|Pz; draw- stealth colorred!!yellow thick dashed scaled cs --+PxXPyXPzX nodemidway above tiny vec r_P; draw- stealth colorolive thick scaled cs PxXPyXPzX--LxX LyX LzX nodemidway above tiny vec d; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesLxXLyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesgxXgyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesPxXPyX; tikzpicture center Normalenvektor von g ablesen: vec n pmatrix tx ty tz pmatrix tx x + ty y + tz z + D P einsetzen und so D bestimmen: hxX+hyX+hzX + D Rightarrow D HX Daraus folgt dann die Ebenengleichung: tx x + tz z HX Normalebene durch P zu g schneiden mit g dafür werden zunächst die Komponentengleichungen von g aufgestellt: center x gx+tx t y gy+ty t z gz+tz t center Anschliess wird der Schnittpunkt S bestimmt: center tx gx+tx t + tz gz+tz t HX ixX+jxX t + izX+jzX t HX lX+mX t t nX Rightarrow S uxX|uyX|uzX center Vergleicht man diesen S mit dem Lotfusspunkt L aus der ersten Berechungsmethode fällt auf dass es sich bei den beiden um den gleichen Punkt handelt. Nun muss nur noch der Abstand zwischen P und S bestimmt werden: vec d vec r_S - vec r_P pmatrix x_S y_S z_S pmatrix - pmatrix x_P y_P z_P pmatrix pmatrix uxX uyX uzX pmatrix - pmatrix PxX PyX PzX pmatrix pmatrix AX BX CX pmatrix |vec d| sqrtx_S-x_P^+y_S-y_P^+z_S-z_P^ sqrtLxX-PxX^+LyX-PyX^+LzX-PzX^ sqrtAX^+BX^+CX^ G
Meta Information
Exercise:
Welchen Abstand hat der Punkt PPx|Py|Pz zu der Geraden g: pmatrix x y z pmatrix pmatrix gx gy gz pmatrix + t pmatrix tx ty tz pmatrix?
Solution:
tikzset glow/.style preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. bf . Berechnungsmethode tdplotsetmaincoords center tikzpicturelatex scale. tdplot_main_coords tikzsetscaled unit vectors. foreach x in -... drawcolorgray scaled cs x---x; foreach y in -... drawcolorgray scaled cs -y--y; drawcolorgreen!!black- scaled cs ---. noderight small bmx; drawcolorgreen!!black- scaled cs ---. nodeabove small bmy; drawcolorgreen!!black- scaled cs --- nodeleft small bmz; drawdotted scaled cs LxX LyX LzX--LxX LyX ; drawdotted scaled cs PxX PyX PzX--PxX PyX ; drawdotted scaled cs gxX gyX gzX--gxX gyX ; drawcolorblue scaled cs gxXgyXgzX--+-*txX-*tyX-*tzX nodeleftsmallg; drawcolorblue scaled cs gxXgyXgzX--+*txX*tyX*tzX; draw- stealth colorred thick scaled cs gxXgyXgzX--+txXtyXtzX nodeleft tiny pmatrix tx ty tzpmatrix vec v; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblue!!white coordinatesgxXgyXgzX noderight tiny Dgx|gy|gz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillviolet!!white coordinatesLxXLyXLzX nodeleftred!!blue tiny L; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillred!!yellow coordinatesPxXPyXPzX noderight red!!yellow tiny PPx|Py|Pz; draw- stealth colorred!!yellow thick dashed scaled cs --+PxXPyXPzX nodemidway above tiny vec r_P; draw- stealth colorred!!blue thick dashed scaled cs --+LxXLyXLzX nodemidway left tiny vec r_L; draw- stealth colorolive thick scaled cs PxXPyXPzX--LxX LyX LzX nodemidway above tiny vec d; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesLxXLyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesgxXgyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesPxXPyX; tikzpicture center Um den Abstand zu berechnen muss als erstes der Lotfusspunkt L auf der Geraden g gefunden werden. Weil der Vektor vecPL rechtwinklig zum Vektor vec v in Richtung der Geraden sein muss deren Skalarprodukt also verschwinden muss gilt: leftvec L - vec Pright vec v &mustbe leftpmatrix L_x L_y L_zpmatrix - pmatrix Px Py Pz pmatrix right pmatrix tx ty tz pmatrix &mustbe Der Punkt L ist unbekannt aber liegt auf der Geraden weshalb man schreiben kann: leftpmatrix gx - t tx gy - t ty gz - t tzpmatrix - pmatrix Px Py Pz pmatrix right pmatrix tx ty tz pmatrix &mustbe pmatrix - t tx - - t ty - - t tzpmatrix pmatrix tx ty tz pmatrix &mustbe Skalarprodukt ausrechnen und auflösen nach t liefert: t . Damit findet man den Lotfusspunkt: pmatrix L_x L_y L_zpmatrix pmatrix gx gy gz pmatrix + . pmatrix tx ty tz pmatrix pmatrix Lx Ly Lz pmatrix Der Abstand zwischen den Punkten L und P kann nun leicht berechnet werden: vec d vec r_L - vec r_P pmatrix x_L y_L z_L pmatrix - pmatrix x_P y_P z_P pmatrix pmatrix LxX LyX LzX pmatrix - pmatrix PxX PyX PzX pmatrix pmatrix AX BX CX pmatrix |vec d| sqrtx_L-x_P^+y_L-y_P^+z_L-z_P^ sqrtLxX-PxX^+LyX-PyX^+LzX-PzX^ sqrtAX^+BX^+CX^ G bf . Berechnungsmethode tdplotsetmaincoords center tikzpicturelatex scale. tdplot_main_coords tikzsetscaled unit vectors. foreach x in -... drawcolorgray scaled cs x---x; foreach y in -... drawcolorgray scaled cs -y--y; drawcolorgreen!!black- scaled cs ---. noderight small bmx; drawcolorgreen!!black- scaled cs ---. nodeabove small bmy; drawcolorgreen!!black- scaled cs --- nodeleft small bmz; drawdotted scaled cs PxX PyX PzX--PxX PyX ; drawdotted scaled cs gxX gyX gzX--gxX gyX ; drawcolorblue scaled cs gxXgyXgzX--+-*txX-*tyX-*tzX nodeleftsmallg; drawcolorblue scaled cs gxXgyXgzX--+*txX*tyX*tzX; draw- stealth colorred thick scaled cs gxXgyXgzX--+txXtyXtzX nodemidwayleft tiny vec v; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblue!!white coordinatesgxX+txXgyX+tyXgzX+tzX nodeleft tiny BBxX|ByX|BzX; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblue!!white coordinatesgxXgyXgzX noderight tiny Agx|gy|gz; draw- stealth colorred!!white dashed thick scaled cs glowred PxXPyXPzX--+txXtyXtzX nodemidway right tiny vec v; draw- stealth colororange!!white dashed thick scaled cs glowyellow gxXgyXgzX--PxXPyXPzX nodemidway below tiny vec AP; draw- stealth colorred!!white dashed thick scaled cs glowyellow BxXByXBzX--+sxXsyXszX; filldrawcolorblack fillyellow!!white opacity. scaled csgxXgyXgzX--BxXByXBzX--QxXQyXQzX--PxXPyXPzX--cycle; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillred!!yellow coordinatesPxXPyXPzX noderight red!!yellow tiny PPx|Py|Pz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblack coordinatesQxXQyXQzX noderight tiny QQxX|QyX|QzX; draw- stealth colorolive thick scaled cs PxXPyXPzX--LxX LyX LzX nodemidway above tiny vec d; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesLxXLyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesgxXgyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesPxXPyX; tikzpicture center Die Fläche des von AB und P aufgespannten Parallelogramms lässt sich darstellen als: F_APQB overlineAB |vec d| Diese Gleichung kann man mithilfe des Kreuzprodukts umformulieren in: F_APQB |vecABtimes vecAP| |vec d| d fracF_APQBoverlineAB d frac|vecABtimes vecAP|overlineAB In diese Formel können nun die konkreten Werte der Aufgabe eingesetzt werden: d fracleft|pmatrix bxX byX bzX pmatrix times pmatrix pxX pyX pzX pmatrixright| overlinepmatrix bxX byX bzX pmatrix fracleft|pmatrix kxX kyX kzX pmatrixright|overlinepmatrix bxX byX bzX pmatrix fracDE F bf . Berechnungsmethode tdplotsetmaincoords center tikzpicturelatex scale. tdplot_main_coords tikzsetscaled unit vectors. foreach x in -... drawcolorgray scaled cs x---x; foreach y in -... drawcolorgray scaled cs -y--y; drawcolorgreen!!black- scaled cs ---. noderight small bmx; drawcolorgreen!!black- scaled cs ---. nodeabove small bmy; drawcolorgreen!!black- scaled cs --- nodeleft small bmz; drawdotted scaled cs LxX LyX LzX--LxX LyX ; drawdotted scaled cs PxX PyX PzX--PxX PyX ; drawdotted scaled cs gxX gyX gzX--gxX gyX ; drawcolorblue scaled cs gxXgyXgzX--+-*txX-*tyX-*tzX nodeleftsmallg; drawcolorblue scaled cs gxXgyXgzX--+*txX*tyX*tzX; drawcoloryellow!!red very thick scaled cs glowyellow --.. nodebelowsmallmathcalE; draw- stealth colorred thick scaled cs gxXgyXgzX--+txXtyXtzX nodeleft tiny pmatrix tx ty tzpmatrix vec v; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblue!!white coordinatesgxXgyXgzX noderight tiny Dgx|gy|gz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillviolet!!white coordinatesLxXLyXLzX nodeleftred!!blue tiny SLx|Ly|Lz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillred!!yellow coordinatesPxXPyXPzX noderight red!!yellow tiny PPx|Py|Pz; draw- stealth colorred!!yellow thick dashed scaled cs --+PxXPyXPzX nodemidway above tiny vec r_P; draw- stealth colorolive thick scaled cs PxXPyXPzX--LxX LyX LzX nodemidway above tiny vec d; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesLxXLyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesgxXgyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesPxXPyX; tikzpicture center Normalenvektor von g ablesen: vec n pmatrix tx ty tz pmatrix tx x + ty y + tz z + D P einsetzen und so D bestimmen: hxX+hyX+hzX + D Rightarrow D HX Daraus folgt dann die Ebenengleichung: tx x + tz z HX Normalebene durch P zu g schneiden mit g dafür werden zunächst die Komponentengleichungen von g aufgestellt: center x gx+tx t y gy+ty t z gz+tz t center Anschliess wird der Schnittpunkt S bestimmt: center tx gx+tx t + tz gz+tz t HX ixX+jxX t + izX+jzX t HX lX+mX t t nX Rightarrow S uxX|uyX|uzX center Vergleicht man diesen S mit dem Lotfusspunkt L aus der ersten Berechungsmethode fällt auf dass es sich bei den beiden um den gleichen Punkt handelt. Nun muss nur noch der Abstand zwischen P und S bestimmt werden: vec d vec r_S - vec r_P pmatrix x_S y_S z_S pmatrix - pmatrix x_P y_P z_P pmatrix pmatrix uxX uyX uzX pmatrix - pmatrix PxX PyX PzX pmatrix pmatrix AX BX CX pmatrix |vec d| sqrtx_S-x_P^+y_S-y_P^+z_S-z_P^ sqrtLxX-PxX^+LyX-PyX^+LzX-PzX^ sqrtAX^+BX^+CX^ G
Welchen Abstand hat der Punkt PPx|Py|Pz zu der Geraden g: pmatrix x y z pmatrix pmatrix gx gy gz pmatrix + t pmatrix tx ty tz pmatrix?
Solution:
tikzset glow/.style preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. preaction# draw line joinround line width.pt opacity. bf . Berechnungsmethode tdplotsetmaincoords center tikzpicturelatex scale. tdplot_main_coords tikzsetscaled unit vectors. foreach x in -... drawcolorgray scaled cs x---x; foreach y in -... drawcolorgray scaled cs -y--y; drawcolorgreen!!black- scaled cs ---. noderight small bmx; drawcolorgreen!!black- scaled cs ---. nodeabove small bmy; drawcolorgreen!!black- scaled cs --- nodeleft small bmz; drawdotted scaled cs LxX LyX LzX--LxX LyX ; drawdotted scaled cs PxX PyX PzX--PxX PyX ; drawdotted scaled cs gxX gyX gzX--gxX gyX ; drawcolorblue scaled cs gxXgyXgzX--+-*txX-*tyX-*tzX nodeleftsmallg; drawcolorblue scaled cs gxXgyXgzX--+*txX*tyX*tzX; draw- stealth colorred thick scaled cs gxXgyXgzX--+txXtyXtzX nodeleft tiny pmatrix tx ty tzpmatrix vec v; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblue!!white coordinatesgxXgyXgzX noderight tiny Dgx|gy|gz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillviolet!!white coordinatesLxXLyXLzX nodeleftred!!blue tiny L; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillred!!yellow coordinatesPxXPyXPzX noderight red!!yellow tiny PPx|Py|Pz; draw- stealth colorred!!yellow thick dashed scaled cs --+PxXPyXPzX nodemidway above tiny vec r_P; draw- stealth colorred!!blue thick dashed scaled cs --+LxXLyXLzX nodemidway left tiny vec r_L; draw- stealth colorolive thick scaled cs PxXPyXPzX--LxX LyX LzX nodemidway above tiny vec d; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesLxXLyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesgxXgyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesPxXPyX; tikzpicture center Um den Abstand zu berechnen muss als erstes der Lotfusspunkt L auf der Geraden g gefunden werden. Weil der Vektor vecPL rechtwinklig zum Vektor vec v in Richtung der Geraden sein muss deren Skalarprodukt also verschwinden muss gilt: leftvec L - vec Pright vec v &mustbe leftpmatrix L_x L_y L_zpmatrix - pmatrix Px Py Pz pmatrix right pmatrix tx ty tz pmatrix &mustbe Der Punkt L ist unbekannt aber liegt auf der Geraden weshalb man schreiben kann: leftpmatrix gx - t tx gy - t ty gz - t tzpmatrix - pmatrix Px Py Pz pmatrix right pmatrix tx ty tz pmatrix &mustbe pmatrix - t tx - - t ty - - t tzpmatrix pmatrix tx ty tz pmatrix &mustbe Skalarprodukt ausrechnen und auflösen nach t liefert: t . Damit findet man den Lotfusspunkt: pmatrix L_x L_y L_zpmatrix pmatrix gx gy gz pmatrix + . pmatrix tx ty tz pmatrix pmatrix Lx Ly Lz pmatrix Der Abstand zwischen den Punkten L und P kann nun leicht berechnet werden: vec d vec r_L - vec r_P pmatrix x_L y_L z_L pmatrix - pmatrix x_P y_P z_P pmatrix pmatrix LxX LyX LzX pmatrix - pmatrix PxX PyX PzX pmatrix pmatrix AX BX CX pmatrix |vec d| sqrtx_L-x_P^+y_L-y_P^+z_L-z_P^ sqrtLxX-PxX^+LyX-PyX^+LzX-PzX^ sqrtAX^+BX^+CX^ G bf . Berechnungsmethode tdplotsetmaincoords center tikzpicturelatex scale. tdplot_main_coords tikzsetscaled unit vectors. foreach x in -... drawcolorgray scaled cs x---x; foreach y in -... drawcolorgray scaled cs -y--y; drawcolorgreen!!black- scaled cs ---. noderight small bmx; drawcolorgreen!!black- scaled cs ---. nodeabove small bmy; drawcolorgreen!!black- scaled cs --- nodeleft small bmz; drawdotted scaled cs PxX PyX PzX--PxX PyX ; drawdotted scaled cs gxX gyX gzX--gxX gyX ; drawcolorblue scaled cs gxXgyXgzX--+-*txX-*tyX-*tzX nodeleftsmallg; drawcolorblue scaled cs gxXgyXgzX--+*txX*tyX*tzX; draw- stealth colorred thick scaled cs gxXgyXgzX--+txXtyXtzX nodemidwayleft tiny vec v; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblue!!white coordinatesgxX+txXgyX+tyXgzX+tzX nodeleft tiny BBxX|ByX|BzX; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblue!!white coordinatesgxXgyXgzX noderight tiny Agx|gy|gz; draw- stealth colorred!!white dashed thick scaled cs glowred PxXPyXPzX--+txXtyXtzX nodemidway right tiny vec v; draw- stealth colororange!!white dashed thick scaled cs glowyellow gxXgyXgzX--PxXPyXPzX nodemidway below tiny vec AP; draw- stealth colorred!!white dashed thick scaled cs glowyellow BxXByXBzX--+sxXsyXszX; filldrawcolorblack fillyellow!!white opacity. scaled csgxXgyXgzX--BxXByXBzX--QxXQyXQzX--PxXPyXPzX--cycle; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillred!!yellow coordinatesPxXPyXPzX noderight red!!yellow tiny PPx|Py|Pz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblack coordinatesQxXQyXQzX noderight tiny QQxX|QyX|QzX; draw- stealth colorolive thick scaled cs PxXPyXPzX--LxX LyX LzX nodemidway above tiny vec d; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesLxXLyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesgxXgyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesPxXPyX; tikzpicture center Die Fläche des von AB und P aufgespannten Parallelogramms lässt sich darstellen als: F_APQB overlineAB |vec d| Diese Gleichung kann man mithilfe des Kreuzprodukts umformulieren in: F_APQB |vecABtimes vecAP| |vec d| d fracF_APQBoverlineAB d frac|vecABtimes vecAP|overlineAB In diese Formel können nun die konkreten Werte der Aufgabe eingesetzt werden: d fracleft|pmatrix bxX byX bzX pmatrix times pmatrix pxX pyX pzX pmatrixright| overlinepmatrix bxX byX bzX pmatrix fracleft|pmatrix kxX kyX kzX pmatrixright|overlinepmatrix bxX byX bzX pmatrix fracDE F bf . Berechnungsmethode tdplotsetmaincoords center tikzpicturelatex scale. tdplot_main_coords tikzsetscaled unit vectors. foreach x in -... drawcolorgray scaled cs x---x; foreach y in -... drawcolorgray scaled cs -y--y; drawcolorgreen!!black- scaled cs ---. noderight small bmx; drawcolorgreen!!black- scaled cs ---. nodeabove small bmy; drawcolorgreen!!black- scaled cs --- nodeleft small bmz; drawdotted scaled cs LxX LyX LzX--LxX LyX ; drawdotted scaled cs PxX PyX PzX--PxX PyX ; drawdotted scaled cs gxX gyX gzX--gxX gyX ; drawcolorblue scaled cs gxXgyXgzX--+-*txX-*tyX-*tzX nodeleftsmallg; drawcolorblue scaled cs gxXgyXgzX--+*txX*tyX*tzX; drawcoloryellow!!red very thick scaled cs glowyellow --.. nodebelowsmallmathcalE; draw- stealth colorred thick scaled cs gxXgyXgzX--+txXtyXtzX nodeleft tiny pmatrix tx ty tzpmatrix vec v; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillblue!!white coordinatesgxXgyXgzX noderight tiny Dgx|gy|gz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillviolet!!white coordinatesLxXLyXLzX nodeleftred!!blue tiny SLx|Ly|Lz; shadedrawscaled cs plot only marks mark* mark sizept mark optionsfillred!!yellow coordinatesPxXPyXPzX noderight red!!yellow tiny PPx|Py|Pz; draw- stealth colorred!!yellow thick dashed scaled cs --+PxXPyXPzX nodemidway above tiny vec r_P; draw- stealth colorolive thick scaled cs PxXPyXPzX--LxX LyX LzX nodemidway above tiny vec d; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesLxXLyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesgxXgyX; shadedrawscaled cs plot only marks mark* mark size.pt mark optionsfillblack coordinatesPxXPyX; tikzpicture center Normalenvektor von g ablesen: vec n pmatrix tx ty tz pmatrix tx x + ty y + tz z + D P einsetzen und so D bestimmen: hxX+hyX+hzX + D Rightarrow D HX Daraus folgt dann die Ebenengleichung: tx x + tz z HX Normalebene durch P zu g schneiden mit g dafür werden zunächst die Komponentengleichungen von g aufgestellt: center x gx+tx t y gy+ty t z gz+tz t center Anschliess wird der Schnittpunkt S bestimmt: center tx gx+tx t + tz gz+tz t HX ixX+jxX t + izX+jzX t HX lX+mX t t nX Rightarrow S uxX|uyX|uzX center Vergleicht man diesen S mit dem Lotfusspunkt L aus der ersten Berechungsmethode fällt auf dass es sich bei den beiden um den gleichen Punkt handelt. Nun muss nur noch der Abstand zwischen P und S bestimmt werden: vec d vec r_S - vec r_P pmatrix x_S y_S z_S pmatrix - pmatrix x_P y_P z_P pmatrix pmatrix uxX uyX uzX pmatrix - pmatrix PxX PyX PzX pmatrix pmatrix AX BX CX pmatrix |vec d| sqrtx_S-x_P^+y_S-y_P^+z_S-z_P^ sqrtLxX-PxX^+LyX-PyX^+LzX-PzX^ sqrtAX^+BX^+CX^ G
Contained in these collections:

