Armbrust
About points...
We associate a certain number of points with each exercise.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
About difficulty...
We associate a certain difficulty with each exercise.
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
Question
Solution
Short
Video
\(\LaTeX\)

Need help? Yes, please!
The following quantities appear in the problem:
Zeit \(t\) / Geschwindigkeit \(v\) / Strecke \(s\) / Beschleunigung \(a\) /
The following formulas must be used to solve the exercise:
\(v = v_0 + at \quad \) \(s = \dfrac{v^2-v_0^2}{2a} \quad \)

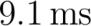
No explanation / solution video to this exercise has yet been created.
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Exercise:
Der Pfeil einer Armbrust wird längs einer cm langen Strecke beschleunigt und verlässt danach die Armbrust mit der Geschwindigkeit . Der Vorgang darf vereinfach als gleichmässig beschleunigte Bewegung angenommen werden. Wie lange dauert die Beschleunigung?
Solution:
newqtystocm newqtystston m newqtyvo newqtyv. % Geg s sto st v vo v % GesZeitt sis % Die Beschleunigung des Pfeils beträgt solqtyafracv^svn**/*stns al a af fracqtyv^st a. % Um mit dieser Beschleunigung aus der Ruhe auf vo zu kommen dauert es solqtytfracsvvn/ans al t fracva fracv^fracvs tf fracva t. % t tf tII Tect- % Bemerkung: Das ist eigentlich die Formel für die Geschwindigkeit bei gleichförmiger Bewegung mit einem zusätzlichen Faktor . Das liegt daran dass der Pfeil der Armbrust zu Beginn still ist -- d.h. sich mit bewegt -- und schliesslich die angegebene Endgeschwindigkeit von v erreicht. Im Durchschnitt ist er also gerade halb so schnell wie am Ende deshalb ist die Zeit auch doppelt so gross wie wenn er die ganze Zeit mit v durch die Armbrust gleiten würde.
Der Pfeil einer Armbrust wird längs einer cm langen Strecke beschleunigt und verlässt danach die Armbrust mit der Geschwindigkeit . Der Vorgang darf vereinfach als gleichmässig beschleunigte Bewegung angenommen werden. Wie lange dauert die Beschleunigung?
Solution:
newqtystocm newqtystston m newqtyvo newqtyv. % Geg s sto st v vo v % GesZeitt sis % Die Beschleunigung des Pfeils beträgt solqtyafracv^svn**/*stns al a af fracqtyv^st a. % Um mit dieser Beschleunigung aus der Ruhe auf vo zu kommen dauert es solqtytfracsvvn/ans al t fracva fracv^fracvs tf fracva t. % t tf tII Tect- % Bemerkung: Das ist eigentlich die Formel für die Geschwindigkeit bei gleichförmiger Bewegung mit einem zusätzlichen Faktor . Das liegt daran dass der Pfeil der Armbrust zu Beginn still ist -- d.h. sich mit bewegt -- und schliesslich die angegebene Endgeschwindigkeit von v erreicht. Im Durchschnitt ist er also gerade halb so schnell wie am Ende deshalb ist die Zeit auch doppelt so gross wie wenn er die ganze Zeit mit v durch die Armbrust gleiten würde.
Meta Information
Exercise:
Der Pfeil einer Armbrust wird längs einer cm langen Strecke beschleunigt und verlässt danach die Armbrust mit der Geschwindigkeit . Der Vorgang darf vereinfach als gleichmässig beschleunigte Bewegung angenommen werden. Wie lange dauert die Beschleunigung?
Solution:
newqtystocm newqtystston m newqtyvo newqtyv. % Geg s sto st v vo v % GesZeitt sis % Die Beschleunigung des Pfeils beträgt solqtyafracv^svn**/*stns al a af fracqtyv^st a. % Um mit dieser Beschleunigung aus der Ruhe auf vo zu kommen dauert es solqtytfracsvvn/ans al t fracva fracv^fracvs tf fracva t. % t tf tII Tect- % Bemerkung: Das ist eigentlich die Formel für die Geschwindigkeit bei gleichförmiger Bewegung mit einem zusätzlichen Faktor . Das liegt daran dass der Pfeil der Armbrust zu Beginn still ist -- d.h. sich mit bewegt -- und schliesslich die angegebene Endgeschwindigkeit von v erreicht. Im Durchschnitt ist er also gerade halb so schnell wie am Ende deshalb ist die Zeit auch doppelt so gross wie wenn er die ganze Zeit mit v durch die Armbrust gleiten würde.
Der Pfeil einer Armbrust wird längs einer cm langen Strecke beschleunigt und verlässt danach die Armbrust mit der Geschwindigkeit . Der Vorgang darf vereinfach als gleichmässig beschleunigte Bewegung angenommen werden. Wie lange dauert die Beschleunigung?
Solution:
newqtystocm newqtystston m newqtyvo newqtyv. % Geg s sto st v vo v % GesZeitt sis % Die Beschleunigung des Pfeils beträgt solqtyafracv^svn**/*stns al a af fracqtyv^st a. % Um mit dieser Beschleunigung aus der Ruhe auf vo zu kommen dauert es solqtytfracsvvn/ans al t fracva fracv^fracvs tf fracva t. % t tf tII Tect- % Bemerkung: Das ist eigentlich die Formel für die Geschwindigkeit bei gleichförmiger Bewegung mit einem zusätzlichen Faktor . Das liegt daran dass der Pfeil der Armbrust zu Beginn still ist -- d.h. sich mit bewegt -- und schliesslich die angegebene Endgeschwindigkeit von v erreicht. Im Durchschnitt ist er also gerade halb so schnell wie am Ende deshalb ist die Zeit auch doppelt so gross wie wenn er die ganze Zeit mit v durch die Armbrust gleiten würde.
Contained in these collections:
-
Beschleunigung 2 by aej
-
Beschleunigung 2 by uz
-
Beschleunigung II by pw
-
Beschleunigung Teil 2 by aej
-
Kinematik - 2. und 3. Formel by TeXercises
Asked Quantity:
Zeit \(t\)
in
Sekunde \(\rm s\)
Physical Quantity
Die Zeit beschreibt die Abfolge von Ereignissen, hat also eine eindeutige, nicht umkehrbare Richtung.
Unit
Seit 1967 ist eine Sekunde das 9.192.631.770-fache der Periodendauer der Strahlung, die dem Übergang zwischen den beiden Hyperfeinstrukturniveaus des Grundzustandes von Atomen des Nuklids 133Cs entspricht.
Base?
SI?
Metric?
Coherent?
Imperial?

