Einfaches Modell eines Generators
About points...
We associate a certain number of points with each exercise.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
About difficulty...
We associate a certain difficulty with each exercise.
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
Question
Solution
Short
Video
\(\LaTeX\)

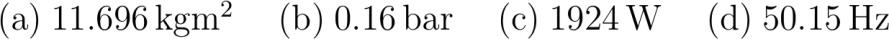
No explanation / solution video to this exercise has yet been created.
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Exercise:
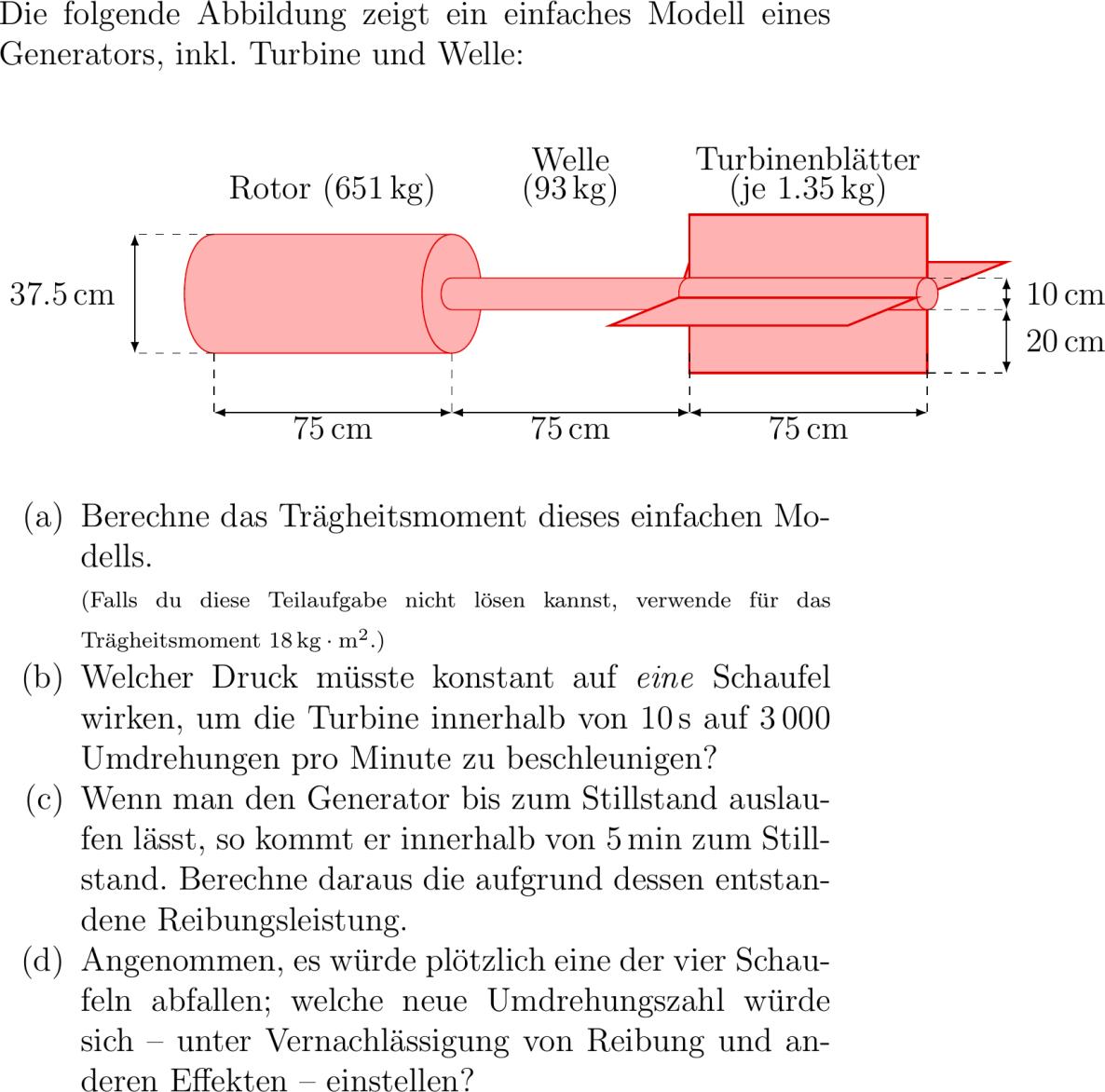
Die folge Abbildung zeigt ein einfaches Modell eines Generators inkl. Turbine und Welle: center tikzpicturelatex % Generator filldrawfillred!!white drawred!!black -. .. controls -.-. and -.. .. .--. .. controls .. and .-. .. -.---.; filldrawfillred!!white drawred!!black . .. controls .. and .-. .. -. .. controls .-. and .. .. .; % Turbine heres Schaufelblatt filldrawfillred!!white drawred!!black thick .--..--.--.--cycle; % Turbine filldrawfillred!!white drawred!!black thick ----.--.--cycle; filldrawfillred!!white drawred!!black thick -------.---.--cycle; % Welle filldrawfillred!!white drawred!!black -. .. controls .-. and .. .. .--. .. controls .. and .-. .. -.---.; filldrawfillred!!white drawred!!black . .. controls .. and .-. .. -. .. controls .-. and .. .. .; drawcolorred!!black . .. controls .. and .-. .. -.;% controls .-. and .. .. .; % Turbine vorderes Schaufelblatt filldrawfillred!!white drawred!!black thick .-.--.-.---.---.--cycle; % Beschriftungen drawdashed -.----.; drawdashed .---.; draw- --.---.; nodeanchoreast at -. pq.cm; drawdashed -.---.; drawdashed .--.; drawdashed ----; draw- -.--.; draw- -.---; nodeanchorwest at . pqcm; nodeanchorwest at .-. pqcm; drawdashed -.---.; drawdashed -.---.; drawdashed -.---.; drawdashed -.---.; draw- -.---.; draw- -.---.; draw- -.---.; node at .-. pqcm; node at .-. pqcm; node at .-. pqcm; node at .. Rotor pqkg; node at .. Welle; node at .. pqkg; node at .. Turbinenblätter; node at .. je pq.kg; tikzpicture center abcliste abc Berechne das Trägheitsmoment dieses einfachen Modells. %Die Dichte von Titan ist pqkgpmk. scriptsize Falls du diese Teilaufgabe nicht lösen kannst verwe für das Trägheitsmoment pqkg m^. abc Welcher Druck müsste konstant auf eine Schaufel wirken um die Turbine innerhalb von pqs auf numpr Umdrehungen pro Minute zu beschleunigen? abc Wenn man den Generator bis zum Stillstand auslaufen lässt so kommt er innerhalb von pqmin zum Stillstand. Berechne daraus die aufgrund dessen entstandene Reibungsleistung. abc Angenommen es würde plötzlich eine der vier Schaufeln abfallen; welche neue Umdrehungszahl würde sich -- unter Vernachlässigung von Reibung und anderen Effekten -- einstellen? abcliste
Solution:
abcliste abc Die Trägheitsmomente des Rotors und der Welle sind einfach zu berechnen: I_R frac m_Rr_^ pq.kgm^ I_W frac m_Wr_^ pq.kgm^ Das Trägheitsmoment einer Schaufel eigentlich ein Quader bezüglich einer Achse durch die Mitte der glqq dünnengrqq Fläche ist: tilde I_S frac m_S a^+b^ frac pq.kg leftpq.m^+pq.m^right pq.kgm^. Die wirkliche Rotationsachse befindet sich aber eine halbe Seite plus den Radius der Stahlwelle von der eben angenommenen entfernt; mit dem Satz von Steiner findet man: I_S tilde I_S + m_S pq.m+pq.m^ pq.kgm^. Das totale Trägheitsmoment des einfachen Generatormodells ist somit: I I_R + I_W + I_S pq.kgm^. abc Um den Generator in der angegebenen Zeit auf die erforderliche Umdrehungszahl zu bringen ist die Winkelbeschleunigung alpha fracomegat pq.rad/s^ erforderlich. Dazu ist das Drehmoment M Ialpha pq.Nm erforderlich. Bei einem mittleren Abstand der Schaufel von pqcm braucht es demnach auf die Schaufel die Kraft F fracMr pqN. Bei einer Fläche von pq.mtimespq.m entspricht das einem durchschnittlichenDruck von p fracFA pqPa pq.bar welcher konstant auf eine Schaufelfläche wirken müsste. abc Der Generator hat im Betrieb eine Rotationsenergie von Erot frac I omega^ pq.eJ. Die Reibungsleistung wäre damit P fracErott pqW. abc Das Trägheitsmoment mit nur drei Schaufeln wäre I'pq.kgm^. Dann gilt Drehimpulserhaltung: L L' Iomega I'omega' omega' fracII'omega f' fracII' f pq.Hz. Die neue Umdrehungszahl wäre demnach numpr. abcliste
Die folge Abbildung zeigt ein einfaches Modell eines Generators inkl. Turbine und Welle: center tikzpicturelatex % Generator filldrawfillred!!white drawred!!black -. .. controls -.-. and -.. .. .--. .. controls .. and .-. .. -.---.; filldrawfillred!!white drawred!!black . .. controls .. and .-. .. -. .. controls .-. and .. .. .; % Turbine heres Schaufelblatt filldrawfillred!!white drawred!!black thick .--..--.--.--cycle; % Turbine filldrawfillred!!white drawred!!black thick ----.--.--cycle; filldrawfillred!!white drawred!!black thick -------.---.--cycle; % Welle filldrawfillred!!white drawred!!black -. .. controls .-. and .. .. .--. .. controls .. and .-. .. -.---.; filldrawfillred!!white drawred!!black . .. controls .. and .-. .. -. .. controls .-. and .. .. .; drawcolorred!!black . .. controls .. and .-. .. -.;% controls .-. and .. .. .; % Turbine vorderes Schaufelblatt filldrawfillred!!white drawred!!black thick .-.--.-.---.---.--cycle; % Beschriftungen drawdashed -.----.; drawdashed .---.; draw- --.---.; nodeanchoreast at -. pq.cm; drawdashed -.---.; drawdashed .--.; drawdashed ----; draw- -.--.; draw- -.---; nodeanchorwest at . pqcm; nodeanchorwest at .-. pqcm; drawdashed -.---.; drawdashed -.---.; drawdashed -.---.; drawdashed -.---.; draw- -.---.; draw- -.---.; draw- -.---.; node at .-. pqcm; node at .-. pqcm; node at .-. pqcm; node at .. Rotor pqkg; node at .. Welle; node at .. pqkg; node at .. Turbinenblätter; node at .. je pq.kg; tikzpicture center abcliste abc Berechne das Trägheitsmoment dieses einfachen Modells. %Die Dichte von Titan ist pqkgpmk. scriptsize Falls du diese Teilaufgabe nicht lösen kannst verwe für das Trägheitsmoment pqkg m^. abc Welcher Druck müsste konstant auf eine Schaufel wirken um die Turbine innerhalb von pqs auf numpr Umdrehungen pro Minute zu beschleunigen? abc Wenn man den Generator bis zum Stillstand auslaufen lässt so kommt er innerhalb von pqmin zum Stillstand. Berechne daraus die aufgrund dessen entstandene Reibungsleistung. abc Angenommen es würde plötzlich eine der vier Schaufeln abfallen; welche neue Umdrehungszahl würde sich -- unter Vernachlässigung von Reibung und anderen Effekten -- einstellen? abcliste
Solution:
abcliste abc Die Trägheitsmomente des Rotors und der Welle sind einfach zu berechnen: I_R frac m_Rr_^ pq.kgm^ I_W frac m_Wr_^ pq.kgm^ Das Trägheitsmoment einer Schaufel eigentlich ein Quader bezüglich einer Achse durch die Mitte der glqq dünnengrqq Fläche ist: tilde I_S frac m_S a^+b^ frac pq.kg leftpq.m^+pq.m^right pq.kgm^. Die wirkliche Rotationsachse befindet sich aber eine halbe Seite plus den Radius der Stahlwelle von der eben angenommenen entfernt; mit dem Satz von Steiner findet man: I_S tilde I_S + m_S pq.m+pq.m^ pq.kgm^. Das totale Trägheitsmoment des einfachen Generatormodells ist somit: I I_R + I_W + I_S pq.kgm^. abc Um den Generator in der angegebenen Zeit auf die erforderliche Umdrehungszahl zu bringen ist die Winkelbeschleunigung alpha fracomegat pq.rad/s^ erforderlich. Dazu ist das Drehmoment M Ialpha pq.Nm erforderlich. Bei einem mittleren Abstand der Schaufel von pqcm braucht es demnach auf die Schaufel die Kraft F fracMr pqN. Bei einer Fläche von pq.mtimespq.m entspricht das einem durchschnittlichenDruck von p fracFA pqPa pq.bar welcher konstant auf eine Schaufelfläche wirken müsste. abc Der Generator hat im Betrieb eine Rotationsenergie von Erot frac I omega^ pq.eJ. Die Reibungsleistung wäre damit P fracErott pqW. abc Das Trägheitsmoment mit nur drei Schaufeln wäre I'pq.kgm^. Dann gilt Drehimpulserhaltung: L L' Iomega I'omega' omega' fracII'omega f' fracII' f pq.Hz. Die neue Umdrehungszahl wäre demnach numpr. abcliste
Meta Information
Exercise:
Die folge Abbildung zeigt ein einfaches Modell eines Generators inkl. Turbine und Welle: center tikzpicturelatex % Generator filldrawfillred!!white drawred!!black -. .. controls -.-. and -.. .. .--. .. controls .. and .-. .. -.---.; filldrawfillred!!white drawred!!black . .. controls .. and .-. .. -. .. controls .-. and .. .. .; % Turbine heres Schaufelblatt filldrawfillred!!white drawred!!black thick .--..--.--.--cycle; % Turbine filldrawfillred!!white drawred!!black thick ----.--.--cycle; filldrawfillred!!white drawred!!black thick -------.---.--cycle; % Welle filldrawfillred!!white drawred!!black -. .. controls .-. and .. .. .--. .. controls .. and .-. .. -.---.; filldrawfillred!!white drawred!!black . .. controls .. and .-. .. -. .. controls .-. and .. .. .; drawcolorred!!black . .. controls .. and .-. .. -.;% controls .-. and .. .. .; % Turbine vorderes Schaufelblatt filldrawfillred!!white drawred!!black thick .-.--.-.---.---.--cycle; % Beschriftungen drawdashed -.----.; drawdashed .---.; draw- --.---.; nodeanchoreast at -. pq.cm; drawdashed -.---.; drawdashed .--.; drawdashed ----; draw- -.--.; draw- -.---; nodeanchorwest at . pqcm; nodeanchorwest at .-. pqcm; drawdashed -.---.; drawdashed -.---.; drawdashed -.---.; drawdashed -.---.; draw- -.---.; draw- -.---.; draw- -.---.; node at .-. pqcm; node at .-. pqcm; node at .-. pqcm; node at .. Rotor pqkg; node at .. Welle; node at .. pqkg; node at .. Turbinenblätter; node at .. je pq.kg; tikzpicture center abcliste abc Berechne das Trägheitsmoment dieses einfachen Modells. %Die Dichte von Titan ist pqkgpmk. scriptsize Falls du diese Teilaufgabe nicht lösen kannst verwe für das Trägheitsmoment pqkg m^. abc Welcher Druck müsste konstant auf eine Schaufel wirken um die Turbine innerhalb von pqs auf numpr Umdrehungen pro Minute zu beschleunigen? abc Wenn man den Generator bis zum Stillstand auslaufen lässt so kommt er innerhalb von pqmin zum Stillstand. Berechne daraus die aufgrund dessen entstandene Reibungsleistung. abc Angenommen es würde plötzlich eine der vier Schaufeln abfallen; welche neue Umdrehungszahl würde sich -- unter Vernachlässigung von Reibung und anderen Effekten -- einstellen? abcliste
Solution:
abcliste abc Die Trägheitsmomente des Rotors und der Welle sind einfach zu berechnen: I_R frac m_Rr_^ pq.kgm^ I_W frac m_Wr_^ pq.kgm^ Das Trägheitsmoment einer Schaufel eigentlich ein Quader bezüglich einer Achse durch die Mitte der glqq dünnengrqq Fläche ist: tilde I_S frac m_S a^+b^ frac pq.kg leftpq.m^+pq.m^right pq.kgm^. Die wirkliche Rotationsachse befindet sich aber eine halbe Seite plus den Radius der Stahlwelle von der eben angenommenen entfernt; mit dem Satz von Steiner findet man: I_S tilde I_S + m_S pq.m+pq.m^ pq.kgm^. Das totale Trägheitsmoment des einfachen Generatormodells ist somit: I I_R + I_W + I_S pq.kgm^. abc Um den Generator in der angegebenen Zeit auf die erforderliche Umdrehungszahl zu bringen ist die Winkelbeschleunigung alpha fracomegat pq.rad/s^ erforderlich. Dazu ist das Drehmoment M Ialpha pq.Nm erforderlich. Bei einem mittleren Abstand der Schaufel von pqcm braucht es demnach auf die Schaufel die Kraft F fracMr pqN. Bei einer Fläche von pq.mtimespq.m entspricht das einem durchschnittlichenDruck von p fracFA pqPa pq.bar welcher konstant auf eine Schaufelfläche wirken müsste. abc Der Generator hat im Betrieb eine Rotationsenergie von Erot frac I omega^ pq.eJ. Die Reibungsleistung wäre damit P fracErott pqW. abc Das Trägheitsmoment mit nur drei Schaufeln wäre I'pq.kgm^. Dann gilt Drehimpulserhaltung: L L' Iomega I'omega' omega' fracII'omega f' fracII' f pq.Hz. Die neue Umdrehungszahl wäre demnach numpr. abcliste
Die folge Abbildung zeigt ein einfaches Modell eines Generators inkl. Turbine und Welle: center tikzpicturelatex % Generator filldrawfillred!!white drawred!!black -. .. controls -.-. and -.. .. .--. .. controls .. and .-. .. -.---.; filldrawfillred!!white drawred!!black . .. controls .. and .-. .. -. .. controls .-. and .. .. .; % Turbine heres Schaufelblatt filldrawfillred!!white drawred!!black thick .--..--.--.--cycle; % Turbine filldrawfillred!!white drawred!!black thick ----.--.--cycle; filldrawfillred!!white drawred!!black thick -------.---.--cycle; % Welle filldrawfillred!!white drawred!!black -. .. controls .-. and .. .. .--. .. controls .. and .-. .. -.---.; filldrawfillred!!white drawred!!black . .. controls .. and .-. .. -. .. controls .-. and .. .. .; drawcolorred!!black . .. controls .. and .-. .. -.;% controls .-. and .. .. .; % Turbine vorderes Schaufelblatt filldrawfillred!!white drawred!!black thick .-.--.-.---.---.--cycle; % Beschriftungen drawdashed -.----.; drawdashed .---.; draw- --.---.; nodeanchoreast at -. pq.cm; drawdashed -.---.; drawdashed .--.; drawdashed ----; draw- -.--.; draw- -.---; nodeanchorwest at . pqcm; nodeanchorwest at .-. pqcm; drawdashed -.---.; drawdashed -.---.; drawdashed -.---.; drawdashed -.---.; draw- -.---.; draw- -.---.; draw- -.---.; node at .-. pqcm; node at .-. pqcm; node at .-. pqcm; node at .. Rotor pqkg; node at .. Welle; node at .. pqkg; node at .. Turbinenblätter; node at .. je pq.kg; tikzpicture center abcliste abc Berechne das Trägheitsmoment dieses einfachen Modells. %Die Dichte von Titan ist pqkgpmk. scriptsize Falls du diese Teilaufgabe nicht lösen kannst verwe für das Trägheitsmoment pqkg m^. abc Welcher Druck müsste konstant auf eine Schaufel wirken um die Turbine innerhalb von pqs auf numpr Umdrehungen pro Minute zu beschleunigen? abc Wenn man den Generator bis zum Stillstand auslaufen lässt so kommt er innerhalb von pqmin zum Stillstand. Berechne daraus die aufgrund dessen entstandene Reibungsleistung. abc Angenommen es würde plötzlich eine der vier Schaufeln abfallen; welche neue Umdrehungszahl würde sich -- unter Vernachlässigung von Reibung und anderen Effekten -- einstellen? abcliste
Solution:
abcliste abc Die Trägheitsmomente des Rotors und der Welle sind einfach zu berechnen: I_R frac m_Rr_^ pq.kgm^ I_W frac m_Wr_^ pq.kgm^ Das Trägheitsmoment einer Schaufel eigentlich ein Quader bezüglich einer Achse durch die Mitte der glqq dünnengrqq Fläche ist: tilde I_S frac m_S a^+b^ frac pq.kg leftpq.m^+pq.m^right pq.kgm^. Die wirkliche Rotationsachse befindet sich aber eine halbe Seite plus den Radius der Stahlwelle von der eben angenommenen entfernt; mit dem Satz von Steiner findet man: I_S tilde I_S + m_S pq.m+pq.m^ pq.kgm^. Das totale Trägheitsmoment des einfachen Generatormodells ist somit: I I_R + I_W + I_S pq.kgm^. abc Um den Generator in der angegebenen Zeit auf die erforderliche Umdrehungszahl zu bringen ist die Winkelbeschleunigung alpha fracomegat pq.rad/s^ erforderlich. Dazu ist das Drehmoment M Ialpha pq.Nm erforderlich. Bei einem mittleren Abstand der Schaufel von pqcm braucht es demnach auf die Schaufel die Kraft F fracMr pqN. Bei einer Fläche von pq.mtimespq.m entspricht das einem durchschnittlichenDruck von p fracFA pqPa pq.bar welcher konstant auf eine Schaufelfläche wirken müsste. abc Der Generator hat im Betrieb eine Rotationsenergie von Erot frac I omega^ pq.eJ. Die Reibungsleistung wäre damit P fracErott pqW. abc Das Trägheitsmoment mit nur drei Schaufeln wäre I'pq.kgm^. Dann gilt Drehimpulserhaltung: L L' Iomega I'omega' omega' fracII'omega f' fracII' f pq.Hz. Die neue Umdrehungszahl wäre demnach numpr. abcliste
Contained in these collections:
-
PAM Matura 2012 Stans by uz

