Experiment von Cavendish
About points...
We associate a certain number of points with each exercise.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
About difficulty...
We associate a certain difficulty with each exercise.
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
Question
Solution
Short
Video
\(\LaTeX\)

No explanation / solution video to this exercise has yet been created.
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Exercise:
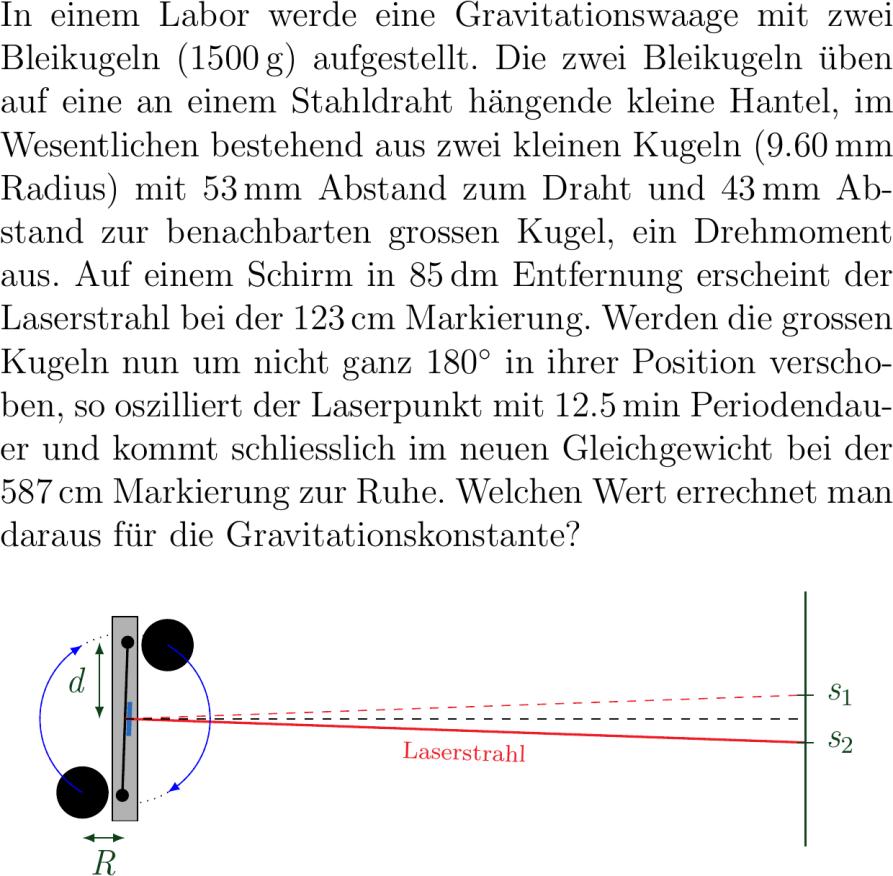
In einem Labor werde eine Gravitationswaage mit zwei Bleikugeln mO aufgestellt. Die zwei Bleikugeln üben auf eine an einem Stahldraht hänge kleine Hantel im Wesentlichen besteh aus zwei kleinen Kugeln rO Radius mit dO Abstand zum Draht und RO Abstand zur benachbarten grossen Kugel ein Drehmoment aus. Auf einem Schirm in LO Entfernung ersche der Laserstrahl bei der saO Markierung. Werden die grossen Kugeln nun um nicht ganz ang in ihrer Position verschoben so oszilliert der Laserpunkt mit TO Periodauer und kommt schliesslich im neuen Gleichgewicht bei der sbO Markierung zur Ruhe. Welchen Wert errechnet man daraus für die Gravitationskonstante? center tikzpicture drawdotted circle cm; filldrawcolorblack :cm circle mm; filldrawcolorblack :cm circle mm; filldrawcolorblack fillblack!!white -.-. rectangle ..; scoperotat drawthick -.--.; filldrawcolorblack -. circle .mm; filldrawcolorblack . circle .mm; drawultra thick colorNavyBlue .-.--..; drawcolorRed thick -- nodemidway below rotat scriptsize Laserstrahl; scope scoperotate drawcolorRed dashed --; scope drawdashed --; drawcolorgreen!!black thick -.--.; drawcolorgreen!!black .-.--.-. noderight s_; drawcolorgreen!!black ..--.. noderight s_; draw-colorgreen!!black -.---.. nodemidway left d; draw-colorgreen!!black -.-.---. nodemidway below R; draw- blue :cm arc ::cm; draw- blue :cm arc :-:cm; tikzpicture center
Solution:
Das Drehmoment welches von den beiden grossen Massen auf die beiden kleinen Massen ausgeübt wird beträgt zusammen genommen: M M_ Fd G fracm_m_R^ d Dieses Drehmoment wird auf den Draht ausgeübt an dem die Hantel hängt. Daher ist dieses Drehmoment auch proportional zum Winkel um welchen der Draht verdreht wird M D phi wobei D das Direktionsmoment bzw. die Torsionskonstante des Drahtes ist. Zusammengenommen und nach der Gravitationskonstante aufgelöst erhält man: G fracm_m_R^ d D phi G fracR^Dphidm_m_ Für kleine Winkel gilt ausserdem thetaapproxtantheta so dass theta &approx fracs_-s_L folgt. Der Winkel um welchen der Draht verdreht wurde ist die Hälfte von diesem Winkel wegen der Reflexion am Spiegel: phi fractheta fracs_-s_L Drückt man nun das Direktionsmoment noch durch die Schwingungsdauer aus also omega sqrtfracDJ D omega^ J fracpi^T^ leftfracm_r^+m_d^right findet man: G fracR^phidm_m_ fracpi^T^ m_leftfracr^+d^right fracR^ fracs_-s_Ldm_m_ fracpi^T^ m_leftfracr^+d^right fracpi^ R^ s_-s_leftfracr^+d^rightdm_LT^ Gexp
In einem Labor werde eine Gravitationswaage mit zwei Bleikugeln mO aufgestellt. Die zwei Bleikugeln üben auf eine an einem Stahldraht hänge kleine Hantel im Wesentlichen besteh aus zwei kleinen Kugeln rO Radius mit dO Abstand zum Draht und RO Abstand zur benachbarten grossen Kugel ein Drehmoment aus. Auf einem Schirm in LO Entfernung ersche der Laserstrahl bei der saO Markierung. Werden die grossen Kugeln nun um nicht ganz ang in ihrer Position verschoben so oszilliert der Laserpunkt mit TO Periodauer und kommt schliesslich im neuen Gleichgewicht bei der sbO Markierung zur Ruhe. Welchen Wert errechnet man daraus für die Gravitationskonstante? center tikzpicture drawdotted circle cm; filldrawcolorblack :cm circle mm; filldrawcolorblack :cm circle mm; filldrawcolorblack fillblack!!white -.-. rectangle ..; scoperotat drawthick -.--.; filldrawcolorblack -. circle .mm; filldrawcolorblack . circle .mm; drawultra thick colorNavyBlue .-.--..; drawcolorRed thick -- nodemidway below rotat scriptsize Laserstrahl; scope scoperotate drawcolorRed dashed --; scope drawdashed --; drawcolorgreen!!black thick -.--.; drawcolorgreen!!black .-.--.-. noderight s_; drawcolorgreen!!black ..--.. noderight s_; draw-colorgreen!!black -.---.. nodemidway left d; draw-colorgreen!!black -.-.---. nodemidway below R; draw- blue :cm arc ::cm; draw- blue :cm arc :-:cm; tikzpicture center
Solution:
Das Drehmoment welches von den beiden grossen Massen auf die beiden kleinen Massen ausgeübt wird beträgt zusammen genommen: M M_ Fd G fracm_m_R^ d Dieses Drehmoment wird auf den Draht ausgeübt an dem die Hantel hängt. Daher ist dieses Drehmoment auch proportional zum Winkel um welchen der Draht verdreht wird M D phi wobei D das Direktionsmoment bzw. die Torsionskonstante des Drahtes ist. Zusammengenommen und nach der Gravitationskonstante aufgelöst erhält man: G fracm_m_R^ d D phi G fracR^Dphidm_m_ Für kleine Winkel gilt ausserdem thetaapproxtantheta so dass theta &approx fracs_-s_L folgt. Der Winkel um welchen der Draht verdreht wurde ist die Hälfte von diesem Winkel wegen der Reflexion am Spiegel: phi fractheta fracs_-s_L Drückt man nun das Direktionsmoment noch durch die Schwingungsdauer aus also omega sqrtfracDJ D omega^ J fracpi^T^ leftfracm_r^+m_d^right findet man: G fracR^phidm_m_ fracpi^T^ m_leftfracr^+d^right fracR^ fracs_-s_Ldm_m_ fracpi^T^ m_leftfracr^+d^right fracpi^ R^ s_-s_leftfracr^+d^rightdm_LT^ Gexp
Meta Information
Exercise:
In einem Labor werde eine Gravitationswaage mit zwei Bleikugeln mO aufgestellt. Die zwei Bleikugeln üben auf eine an einem Stahldraht hänge kleine Hantel im Wesentlichen besteh aus zwei kleinen Kugeln rO Radius mit dO Abstand zum Draht und RO Abstand zur benachbarten grossen Kugel ein Drehmoment aus. Auf einem Schirm in LO Entfernung ersche der Laserstrahl bei der saO Markierung. Werden die grossen Kugeln nun um nicht ganz ang in ihrer Position verschoben so oszilliert der Laserpunkt mit TO Periodauer und kommt schliesslich im neuen Gleichgewicht bei der sbO Markierung zur Ruhe. Welchen Wert errechnet man daraus für die Gravitationskonstante? center tikzpicture drawdotted circle cm; filldrawcolorblack :cm circle mm; filldrawcolorblack :cm circle mm; filldrawcolorblack fillblack!!white -.-. rectangle ..; scoperotat drawthick -.--.; filldrawcolorblack -. circle .mm; filldrawcolorblack . circle .mm; drawultra thick colorNavyBlue .-.--..; drawcolorRed thick -- nodemidway below rotat scriptsize Laserstrahl; scope scoperotate drawcolorRed dashed --; scope drawdashed --; drawcolorgreen!!black thick -.--.; drawcolorgreen!!black .-.--.-. noderight s_; drawcolorgreen!!black ..--.. noderight s_; draw-colorgreen!!black -.---.. nodemidway left d; draw-colorgreen!!black -.-.---. nodemidway below R; draw- blue :cm arc ::cm; draw- blue :cm arc :-:cm; tikzpicture center
Solution:
Das Drehmoment welches von den beiden grossen Massen auf die beiden kleinen Massen ausgeübt wird beträgt zusammen genommen: M M_ Fd G fracm_m_R^ d Dieses Drehmoment wird auf den Draht ausgeübt an dem die Hantel hängt. Daher ist dieses Drehmoment auch proportional zum Winkel um welchen der Draht verdreht wird M D phi wobei D das Direktionsmoment bzw. die Torsionskonstante des Drahtes ist. Zusammengenommen und nach der Gravitationskonstante aufgelöst erhält man: G fracm_m_R^ d D phi G fracR^Dphidm_m_ Für kleine Winkel gilt ausserdem thetaapproxtantheta so dass theta &approx fracs_-s_L folgt. Der Winkel um welchen der Draht verdreht wurde ist die Hälfte von diesem Winkel wegen der Reflexion am Spiegel: phi fractheta fracs_-s_L Drückt man nun das Direktionsmoment noch durch die Schwingungsdauer aus also omega sqrtfracDJ D omega^ J fracpi^T^ leftfracm_r^+m_d^right findet man: G fracR^phidm_m_ fracpi^T^ m_leftfracr^+d^right fracR^ fracs_-s_Ldm_m_ fracpi^T^ m_leftfracr^+d^right fracpi^ R^ s_-s_leftfracr^+d^rightdm_LT^ Gexp
In einem Labor werde eine Gravitationswaage mit zwei Bleikugeln mO aufgestellt. Die zwei Bleikugeln üben auf eine an einem Stahldraht hänge kleine Hantel im Wesentlichen besteh aus zwei kleinen Kugeln rO Radius mit dO Abstand zum Draht und RO Abstand zur benachbarten grossen Kugel ein Drehmoment aus. Auf einem Schirm in LO Entfernung ersche der Laserstrahl bei der saO Markierung. Werden die grossen Kugeln nun um nicht ganz ang in ihrer Position verschoben so oszilliert der Laserpunkt mit TO Periodauer und kommt schliesslich im neuen Gleichgewicht bei der sbO Markierung zur Ruhe. Welchen Wert errechnet man daraus für die Gravitationskonstante? center tikzpicture drawdotted circle cm; filldrawcolorblack :cm circle mm; filldrawcolorblack :cm circle mm; filldrawcolorblack fillblack!!white -.-. rectangle ..; scoperotat drawthick -.--.; filldrawcolorblack -. circle .mm; filldrawcolorblack . circle .mm; drawultra thick colorNavyBlue .-.--..; drawcolorRed thick -- nodemidway below rotat scriptsize Laserstrahl; scope scoperotate drawcolorRed dashed --; scope drawdashed --; drawcolorgreen!!black thick -.--.; drawcolorgreen!!black .-.--.-. noderight s_; drawcolorgreen!!black ..--.. noderight s_; draw-colorgreen!!black -.---.. nodemidway left d; draw-colorgreen!!black -.-.---. nodemidway below R; draw- blue :cm arc ::cm; draw- blue :cm arc :-:cm; tikzpicture center
Solution:
Das Drehmoment welches von den beiden grossen Massen auf die beiden kleinen Massen ausgeübt wird beträgt zusammen genommen: M M_ Fd G fracm_m_R^ d Dieses Drehmoment wird auf den Draht ausgeübt an dem die Hantel hängt. Daher ist dieses Drehmoment auch proportional zum Winkel um welchen der Draht verdreht wird M D phi wobei D das Direktionsmoment bzw. die Torsionskonstante des Drahtes ist. Zusammengenommen und nach der Gravitationskonstante aufgelöst erhält man: G fracm_m_R^ d D phi G fracR^Dphidm_m_ Für kleine Winkel gilt ausserdem thetaapproxtantheta so dass theta &approx fracs_-s_L folgt. Der Winkel um welchen der Draht verdreht wurde ist die Hälfte von diesem Winkel wegen der Reflexion am Spiegel: phi fractheta fracs_-s_L Drückt man nun das Direktionsmoment noch durch die Schwingungsdauer aus also omega sqrtfracDJ D omega^ J fracpi^T^ leftfracm_r^+m_d^right findet man: G fracR^phidm_m_ fracpi^T^ m_leftfracr^+d^right fracR^ fracs_-s_Ldm_m_ fracpi^T^ m_leftfracr^+d^right fracpi^ R^ s_-s_leftfracr^+d^rightdm_LT^ Gexp
Contained in these collections:
-
Harmonische Schwingung 3 by uz

