Fadenrolle
About points...
We associate a certain number of points with each exercise.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
About difficulty...
We associate a certain difficulty with each exercise.
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
Question
Solution
Short
Video
\(\LaTeX\)
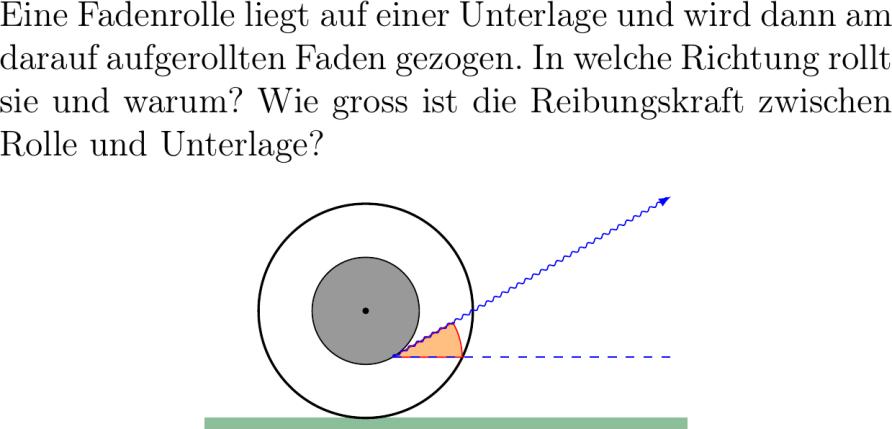

Exercise:
Eine Fadenrolle liegt auf einer Unterlage und wird dann am darauf aufgerollten Faden gezogen. In welche Richtung rollt sie und warum? Wie gross ist die Reibungskraft zwischen Rolle und Unterlage? center tikzpicturescale. latex filldrawcolorgreen!!white fillgreen!!white - rectangle -.; drawthick circle cm; filldrawcolorred fillorange!!white ++-:cm--+. arc ::.cm -- cycle; filldrawcolorblack fillblack!!white circle cm; filldrawcolorblack fillblack circle .mm; drawsnakecoilsegment aspect segment amplitude.pt segment lengthpt colorblue - ++-:cm -- ++:; drawcolorblue dashed ++-:cm--+.; tikzpicture center
Solution:
Die Fadenspule und die wirken Kräfte sind in der folgen Skizze abgebildet: center tikzpicturescale. latex filldrawcolorgreen!!white fillgreen!!white - rectangle -.; drawthick circle cm; filldrawcolorblack fillblack!!white circle cm; filldrawcolorblack fillblack circle .mm; filldrawcolorred fillorange!!white ++-:cm--+. arc ::.cm -- cycle; draw- green!!black -- ++:cm nodemidway above R; draw- green!!black -- ++:cm nodemidway below r; drawsnakecoilsegment aspect segment amplitude.pt segment lengthpt colorblue - ++-:cm -- ++:; nodecolorblue at . F; nodecolororange at .. theta; draw-colorblue dashed ++-:cm--+. noderight F_rightarrow; draw- colorred thick ---; nodecolorred at -.. FR; tikzpicture center In y-Richtung herrscht Kräftegleichgewicht; die Unterlage wird zusammen mit der vertikalen Komponente der Zugkraft die Gravitation kompensieren. Ebenso gilt dass die Reibung und die horizontale Komponente der Zugkraft die Beschleunigung der Fadenspule in x-Richtung bestimmen das was uns eressiert: ma F_rightarrow - FR F costheta -FR Die beiden wirken Drehmomente eines kommt von der Zugkraft eines von der Reibung bestimmen zusammen die Winkelbeschleunigung der Fadenspule d.h.: Jalpha M_ + M_ R FR - r F Ausserdem ist es so dass die Beschleunigung der Translationsbewegung also a in x-Richtung mit der Winkelbeschleunigung zusammenhängt solange die Fadenspule schlupffrei rollt: a Ralpha Nun ist es reine Mathematik. Auflösen nach der gesuchten Beschleunigung a. Alle drei Gleichungen kombiniert führt auf: J fracaR R FR - r F Ja R^ Fcostheta-ma - Rr F a fracRcostheta-r RJ+mR^ F Kritischer Term: Rcostheta-r dessen Vorzeichen bestimmt Richtung.
Eine Fadenrolle liegt auf einer Unterlage und wird dann am darauf aufgerollten Faden gezogen. In welche Richtung rollt sie und warum? Wie gross ist die Reibungskraft zwischen Rolle und Unterlage? center tikzpicturescale. latex filldrawcolorgreen!!white fillgreen!!white - rectangle -.; drawthick circle cm; filldrawcolorred fillorange!!white ++-:cm--+. arc ::.cm -- cycle; filldrawcolorblack fillblack!!white circle cm; filldrawcolorblack fillblack circle .mm; drawsnakecoilsegment aspect segment amplitude.pt segment lengthpt colorblue - ++-:cm -- ++:; drawcolorblue dashed ++-:cm--+.; tikzpicture center
Solution:
Die Fadenspule und die wirken Kräfte sind in der folgen Skizze abgebildet: center tikzpicturescale. latex filldrawcolorgreen!!white fillgreen!!white - rectangle -.; drawthick circle cm; filldrawcolorblack fillblack!!white circle cm; filldrawcolorblack fillblack circle .mm; filldrawcolorred fillorange!!white ++-:cm--+. arc ::.cm -- cycle; draw- green!!black -- ++:cm nodemidway above R; draw- green!!black -- ++:cm nodemidway below r; drawsnakecoilsegment aspect segment amplitude.pt segment lengthpt colorblue - ++-:cm -- ++:; nodecolorblue at . F; nodecolororange at .. theta; draw-colorblue dashed ++-:cm--+. noderight F_rightarrow; draw- colorred thick ---; nodecolorred at -.. FR; tikzpicture center In y-Richtung herrscht Kräftegleichgewicht; die Unterlage wird zusammen mit der vertikalen Komponente der Zugkraft die Gravitation kompensieren. Ebenso gilt dass die Reibung und die horizontale Komponente der Zugkraft die Beschleunigung der Fadenspule in x-Richtung bestimmen das was uns eressiert: ma F_rightarrow - FR F costheta -FR Die beiden wirken Drehmomente eines kommt von der Zugkraft eines von der Reibung bestimmen zusammen die Winkelbeschleunigung der Fadenspule d.h.: Jalpha M_ + M_ R FR - r F Ausserdem ist es so dass die Beschleunigung der Translationsbewegung also a in x-Richtung mit der Winkelbeschleunigung zusammenhängt solange die Fadenspule schlupffrei rollt: a Ralpha Nun ist es reine Mathematik. Auflösen nach der gesuchten Beschleunigung a. Alle drei Gleichungen kombiniert führt auf: J fracaR R FR - r F Ja R^ Fcostheta-ma - Rr F a fracRcostheta-r RJ+mR^ F Kritischer Term: Rcostheta-r dessen Vorzeichen bestimmt Richtung.
Meta Information
Exercise:
Eine Fadenrolle liegt auf einer Unterlage und wird dann am darauf aufgerollten Faden gezogen. In welche Richtung rollt sie und warum? Wie gross ist die Reibungskraft zwischen Rolle und Unterlage? center tikzpicturescale. latex filldrawcolorgreen!!white fillgreen!!white - rectangle -.; drawthick circle cm; filldrawcolorred fillorange!!white ++-:cm--+. arc ::.cm -- cycle; filldrawcolorblack fillblack!!white circle cm; filldrawcolorblack fillblack circle .mm; drawsnakecoilsegment aspect segment amplitude.pt segment lengthpt colorblue - ++-:cm -- ++:; drawcolorblue dashed ++-:cm--+.; tikzpicture center
Solution:
Die Fadenspule und die wirken Kräfte sind in der folgen Skizze abgebildet: center tikzpicturescale. latex filldrawcolorgreen!!white fillgreen!!white - rectangle -.; drawthick circle cm; filldrawcolorblack fillblack!!white circle cm; filldrawcolorblack fillblack circle .mm; filldrawcolorred fillorange!!white ++-:cm--+. arc ::.cm -- cycle; draw- green!!black -- ++:cm nodemidway above R; draw- green!!black -- ++:cm nodemidway below r; drawsnakecoilsegment aspect segment amplitude.pt segment lengthpt colorblue - ++-:cm -- ++:; nodecolorblue at . F; nodecolororange at .. theta; draw-colorblue dashed ++-:cm--+. noderight F_rightarrow; draw- colorred thick ---; nodecolorred at -.. FR; tikzpicture center In y-Richtung herrscht Kräftegleichgewicht; die Unterlage wird zusammen mit der vertikalen Komponente der Zugkraft die Gravitation kompensieren. Ebenso gilt dass die Reibung und die horizontale Komponente der Zugkraft die Beschleunigung der Fadenspule in x-Richtung bestimmen das was uns eressiert: ma F_rightarrow - FR F costheta -FR Die beiden wirken Drehmomente eines kommt von der Zugkraft eines von der Reibung bestimmen zusammen die Winkelbeschleunigung der Fadenspule d.h.: Jalpha M_ + M_ R FR - r F Ausserdem ist es so dass die Beschleunigung der Translationsbewegung also a in x-Richtung mit der Winkelbeschleunigung zusammenhängt solange die Fadenspule schlupffrei rollt: a Ralpha Nun ist es reine Mathematik. Auflösen nach der gesuchten Beschleunigung a. Alle drei Gleichungen kombiniert führt auf: J fracaR R FR - r F Ja R^ Fcostheta-ma - Rr F a fracRcostheta-r RJ+mR^ F Kritischer Term: Rcostheta-r dessen Vorzeichen bestimmt Richtung.
Eine Fadenrolle liegt auf einer Unterlage und wird dann am darauf aufgerollten Faden gezogen. In welche Richtung rollt sie und warum? Wie gross ist die Reibungskraft zwischen Rolle und Unterlage? center tikzpicturescale. latex filldrawcolorgreen!!white fillgreen!!white - rectangle -.; drawthick circle cm; filldrawcolorred fillorange!!white ++-:cm--+. arc ::.cm -- cycle; filldrawcolorblack fillblack!!white circle cm; filldrawcolorblack fillblack circle .mm; drawsnakecoilsegment aspect segment amplitude.pt segment lengthpt colorblue - ++-:cm -- ++:; drawcolorblue dashed ++-:cm--+.; tikzpicture center
Solution:
Die Fadenspule und die wirken Kräfte sind in der folgen Skizze abgebildet: center tikzpicturescale. latex filldrawcolorgreen!!white fillgreen!!white - rectangle -.; drawthick circle cm; filldrawcolorblack fillblack!!white circle cm; filldrawcolorblack fillblack circle .mm; filldrawcolorred fillorange!!white ++-:cm--+. arc ::.cm -- cycle; draw- green!!black -- ++:cm nodemidway above R; draw- green!!black -- ++:cm nodemidway below r; drawsnakecoilsegment aspect segment amplitude.pt segment lengthpt colorblue - ++-:cm -- ++:; nodecolorblue at . F; nodecolororange at .. theta; draw-colorblue dashed ++-:cm--+. noderight F_rightarrow; draw- colorred thick ---; nodecolorred at -.. FR; tikzpicture center In y-Richtung herrscht Kräftegleichgewicht; die Unterlage wird zusammen mit der vertikalen Komponente der Zugkraft die Gravitation kompensieren. Ebenso gilt dass die Reibung und die horizontale Komponente der Zugkraft die Beschleunigung der Fadenspule in x-Richtung bestimmen das was uns eressiert: ma F_rightarrow - FR F costheta -FR Die beiden wirken Drehmomente eines kommt von der Zugkraft eines von der Reibung bestimmen zusammen die Winkelbeschleunigung der Fadenspule d.h.: Jalpha M_ + M_ R FR - r F Ausserdem ist es so dass die Beschleunigung der Translationsbewegung also a in x-Richtung mit der Winkelbeschleunigung zusammenhängt solange die Fadenspule schlupffrei rollt: a Ralpha Nun ist es reine Mathematik. Auflösen nach der gesuchten Beschleunigung a. Alle drei Gleichungen kombiniert führt auf: J fracaR R FR - r F Ja R^ Fcostheta-ma - Rr F a fracRcostheta-r RJ+mR^ F Kritischer Term: Rcostheta-r dessen Vorzeichen bestimmt Richtung.
Linked Clicker question: Fadenrolle
Contained in these collections:
-
-
ETH 1. Vordiplom Physik Frühling 1996 by TeXercises
-

