Feldwürfel
About points...
We associate a certain number of points with each exercise.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
About difficulty...
We associate a certain difficulty with each exercise.
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
Question
Solution
Short
Video
\(\LaTeX\)

No explanation / solution video to this exercise has yet been created.
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Exercise:
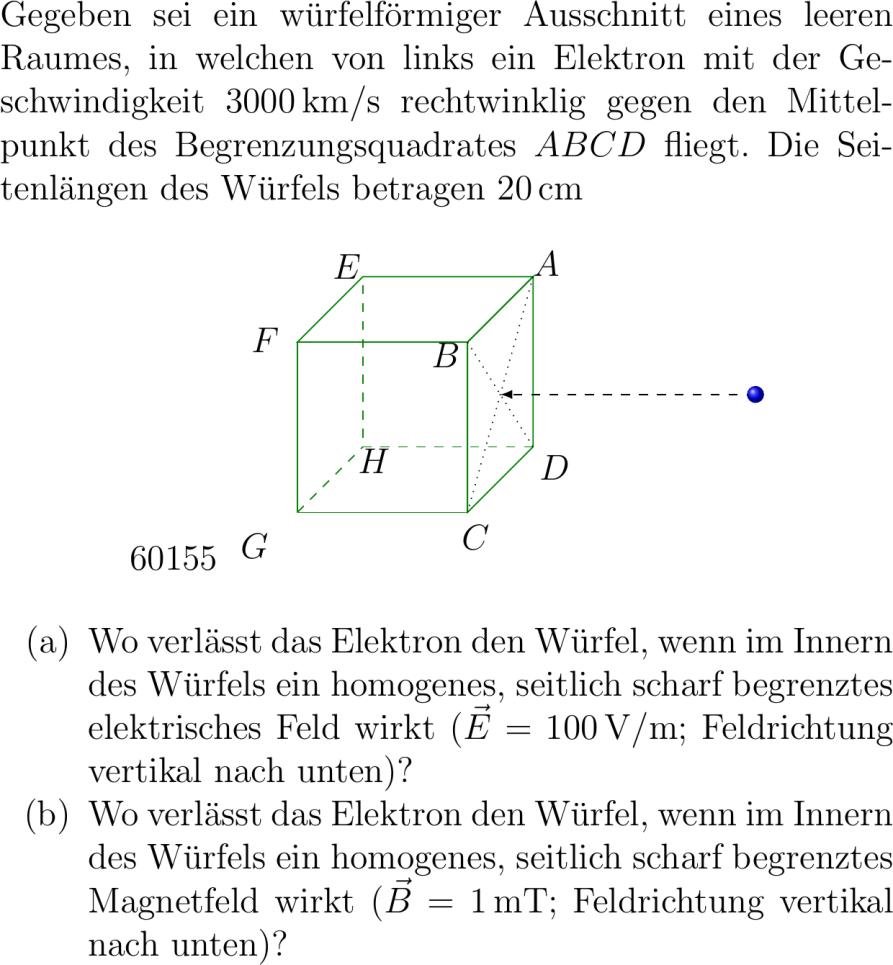
Gegeben sei ein würfelförmiger Ausschnitt eines leeren Raumes in welchen von links ein Elektron mit der Geschwindigkeit pqkm/s rechtwinklig gegen den Mittelpunkt des Begrenzungsquadrates ABCD fliegt. Die Seitenlängen des Würfels betragen pqcm center tdplotsetmaincoords tikzpicturelatextdplot_main_coords cube/.stylevery thickblack grid/.stylevery thingray axis/.stylbluethick pgfmathsetmacrocubex pgfmathsetmacrocubey pgfmathsetmacrocubez drawcolorgreen!!black -- ++-cubex -- ++-cubey -- ++cubex -- cycle; drawcolorgreen!!black -- ++-cubez -- ++-cubey -- ++cubez -- cycle; drawcolorgreen!!black -- ++-cubex -- ++-cubez -- ++cubex -- cycle; drawdashed- ------; shade ball colorblue -- circle radius.cm; drawcolorgreen!!black dashed -cubey-cubez -- -cubex-cubey-cubez---cubex-cubez; drawcolorgreen!!black dashed -cubex-cubey -- -cubex-cubey-cubez; node at -. A; node at -.. B; node at .-. C; node at .-.-. D; node at -.-. E; node at -... F; node at -.-. G; node at -.-.-. H; drawdotted ----; drawdotted ----; tikzpicture center enumerate itema Wo verlässt das Elektron den Würfel wenn im Innern des Würfels ein homogenes seitlich scharf begrenztes elektrisches Feld wirkt vec E pqV/m; Feldrichtung vertikal nach unten? itemb Wo verlässt das Elektron den Würfel wenn im Innern des Würfels ein homogenes seitlich scharf begrenztes Magnetfeld wirkt vec B pqmT; Feldrichtung vertikal nach unten? enumerate
Solution:
enumerate itema Wenn ein elektrisches Feld von oben nach unten wirkt so bewegt sich das negativ geladene Elektron nach oben. Es wird den Würfel also durch das Quadrat BCGF verlassen; irgwo auf der Linie welche die Seite DC und FG teilt. Es bleibt noch zu klären wo genau; wir nennen diese Stelle s_x. Dafür ist zu berechnen welche Kraft aufgrund des elektrischen Feldes auf das Elektron wirkt: F q vec E pq.N Aufgrund dieser Kraft wird das Elektron beschleunigt: a fracFm pq.eq Mit dieser Beschleunigung muss das Elektron eine halbe Seitenlänge also fracs nach oben zurücklegen; damit kann die Zeit bestimmt werden zu welcher das Elektron wieder aus dem Würfel austritt: t sqrtfracsa pq.s Schliesslich berechnen wir s_x: s_x v t pq.m itemb Wenn die Magnetfeldrichtung nach unten zeigt so wird das Elektron aufgrund der Lorentzkraft auf eine Kreisbahn gelenkt; mit der Dreifingerregel findet man die Richtung des Kreises. Das Elektron wird den Würfel durch das Quadrat ABFE verlassen Achtung: Elektron negativ geladen vec F qvec v times vec B. Die Kreisbahn auf welcher sich das Elektron bewegen wird hat den folgen Radius: r fracmvqB pq.m enumerate
Gegeben sei ein würfelförmiger Ausschnitt eines leeren Raumes in welchen von links ein Elektron mit der Geschwindigkeit pqkm/s rechtwinklig gegen den Mittelpunkt des Begrenzungsquadrates ABCD fliegt. Die Seitenlängen des Würfels betragen pqcm center tdplotsetmaincoords tikzpicturelatextdplot_main_coords cube/.stylevery thickblack grid/.stylevery thingray axis/.stylbluethick pgfmathsetmacrocubex pgfmathsetmacrocubey pgfmathsetmacrocubez drawcolorgreen!!black -- ++-cubex -- ++-cubey -- ++cubex -- cycle; drawcolorgreen!!black -- ++-cubez -- ++-cubey -- ++cubez -- cycle; drawcolorgreen!!black -- ++-cubex -- ++-cubez -- ++cubex -- cycle; drawdashed- ------; shade ball colorblue -- circle radius.cm; drawcolorgreen!!black dashed -cubey-cubez -- -cubex-cubey-cubez---cubex-cubez; drawcolorgreen!!black dashed -cubex-cubey -- -cubex-cubey-cubez; node at -. A; node at -.. B; node at .-. C; node at .-.-. D; node at -.-. E; node at -... F; node at -.-. G; node at -.-.-. H; drawdotted ----; drawdotted ----; tikzpicture center enumerate itema Wo verlässt das Elektron den Würfel wenn im Innern des Würfels ein homogenes seitlich scharf begrenztes elektrisches Feld wirkt vec E pqV/m; Feldrichtung vertikal nach unten? itemb Wo verlässt das Elektron den Würfel wenn im Innern des Würfels ein homogenes seitlich scharf begrenztes Magnetfeld wirkt vec B pqmT; Feldrichtung vertikal nach unten? enumerate
Solution:
enumerate itema Wenn ein elektrisches Feld von oben nach unten wirkt so bewegt sich das negativ geladene Elektron nach oben. Es wird den Würfel also durch das Quadrat BCGF verlassen; irgwo auf der Linie welche die Seite DC und FG teilt. Es bleibt noch zu klären wo genau; wir nennen diese Stelle s_x. Dafür ist zu berechnen welche Kraft aufgrund des elektrischen Feldes auf das Elektron wirkt: F q vec E pq.N Aufgrund dieser Kraft wird das Elektron beschleunigt: a fracFm pq.eq Mit dieser Beschleunigung muss das Elektron eine halbe Seitenlänge also fracs nach oben zurücklegen; damit kann die Zeit bestimmt werden zu welcher das Elektron wieder aus dem Würfel austritt: t sqrtfracsa pq.s Schliesslich berechnen wir s_x: s_x v t pq.m itemb Wenn die Magnetfeldrichtung nach unten zeigt so wird das Elektron aufgrund der Lorentzkraft auf eine Kreisbahn gelenkt; mit der Dreifingerregel findet man die Richtung des Kreises. Das Elektron wird den Würfel durch das Quadrat ABFE verlassen Achtung: Elektron negativ geladen vec F qvec v times vec B. Die Kreisbahn auf welcher sich das Elektron bewegen wird hat den folgen Radius: r fracmvqB pq.m enumerate
Meta Information
Exercise:
Gegeben sei ein würfelförmiger Ausschnitt eines leeren Raumes in welchen von links ein Elektron mit der Geschwindigkeit pqkm/s rechtwinklig gegen den Mittelpunkt des Begrenzungsquadrates ABCD fliegt. Die Seitenlängen des Würfels betragen pqcm center tdplotsetmaincoords tikzpicturelatextdplot_main_coords cube/.stylevery thickblack grid/.stylevery thingray axis/.stylbluethick pgfmathsetmacrocubex pgfmathsetmacrocubey pgfmathsetmacrocubez drawcolorgreen!!black -- ++-cubex -- ++-cubey -- ++cubex -- cycle; drawcolorgreen!!black -- ++-cubez -- ++-cubey -- ++cubez -- cycle; drawcolorgreen!!black -- ++-cubex -- ++-cubez -- ++cubex -- cycle; drawdashed- ------; shade ball colorblue -- circle radius.cm; drawcolorgreen!!black dashed -cubey-cubez -- -cubex-cubey-cubez---cubex-cubez; drawcolorgreen!!black dashed -cubex-cubey -- -cubex-cubey-cubez; node at -. A; node at -.. B; node at .-. C; node at .-.-. D; node at -.-. E; node at -... F; node at -.-. G; node at -.-.-. H; drawdotted ----; drawdotted ----; tikzpicture center enumerate itema Wo verlässt das Elektron den Würfel wenn im Innern des Würfels ein homogenes seitlich scharf begrenztes elektrisches Feld wirkt vec E pqV/m; Feldrichtung vertikal nach unten? itemb Wo verlässt das Elektron den Würfel wenn im Innern des Würfels ein homogenes seitlich scharf begrenztes Magnetfeld wirkt vec B pqmT; Feldrichtung vertikal nach unten? enumerate
Solution:
enumerate itema Wenn ein elektrisches Feld von oben nach unten wirkt so bewegt sich das negativ geladene Elektron nach oben. Es wird den Würfel also durch das Quadrat BCGF verlassen; irgwo auf der Linie welche die Seite DC und FG teilt. Es bleibt noch zu klären wo genau; wir nennen diese Stelle s_x. Dafür ist zu berechnen welche Kraft aufgrund des elektrischen Feldes auf das Elektron wirkt: F q vec E pq.N Aufgrund dieser Kraft wird das Elektron beschleunigt: a fracFm pq.eq Mit dieser Beschleunigung muss das Elektron eine halbe Seitenlänge also fracs nach oben zurücklegen; damit kann die Zeit bestimmt werden zu welcher das Elektron wieder aus dem Würfel austritt: t sqrtfracsa pq.s Schliesslich berechnen wir s_x: s_x v t pq.m itemb Wenn die Magnetfeldrichtung nach unten zeigt so wird das Elektron aufgrund der Lorentzkraft auf eine Kreisbahn gelenkt; mit der Dreifingerregel findet man die Richtung des Kreises. Das Elektron wird den Würfel durch das Quadrat ABFE verlassen Achtung: Elektron negativ geladen vec F qvec v times vec B. Die Kreisbahn auf welcher sich das Elektron bewegen wird hat den folgen Radius: r fracmvqB pq.m enumerate
Gegeben sei ein würfelförmiger Ausschnitt eines leeren Raumes in welchen von links ein Elektron mit der Geschwindigkeit pqkm/s rechtwinklig gegen den Mittelpunkt des Begrenzungsquadrates ABCD fliegt. Die Seitenlängen des Würfels betragen pqcm center tdplotsetmaincoords tikzpicturelatextdplot_main_coords cube/.stylevery thickblack grid/.stylevery thingray axis/.stylbluethick pgfmathsetmacrocubex pgfmathsetmacrocubey pgfmathsetmacrocubez drawcolorgreen!!black -- ++-cubex -- ++-cubey -- ++cubex -- cycle; drawcolorgreen!!black -- ++-cubez -- ++-cubey -- ++cubez -- cycle; drawcolorgreen!!black -- ++-cubex -- ++-cubez -- ++cubex -- cycle; drawdashed- ------; shade ball colorblue -- circle radius.cm; drawcolorgreen!!black dashed -cubey-cubez -- -cubex-cubey-cubez---cubex-cubez; drawcolorgreen!!black dashed -cubex-cubey -- -cubex-cubey-cubez; node at -. A; node at -.. B; node at .-. C; node at .-.-. D; node at -.-. E; node at -... F; node at -.-. G; node at -.-.-. H; drawdotted ----; drawdotted ----; tikzpicture center enumerate itema Wo verlässt das Elektron den Würfel wenn im Innern des Würfels ein homogenes seitlich scharf begrenztes elektrisches Feld wirkt vec E pqV/m; Feldrichtung vertikal nach unten? itemb Wo verlässt das Elektron den Würfel wenn im Innern des Würfels ein homogenes seitlich scharf begrenztes Magnetfeld wirkt vec B pqmT; Feldrichtung vertikal nach unten? enumerate
Solution:
enumerate itema Wenn ein elektrisches Feld von oben nach unten wirkt so bewegt sich das negativ geladene Elektron nach oben. Es wird den Würfel also durch das Quadrat BCGF verlassen; irgwo auf der Linie welche die Seite DC und FG teilt. Es bleibt noch zu klären wo genau; wir nennen diese Stelle s_x. Dafür ist zu berechnen welche Kraft aufgrund des elektrischen Feldes auf das Elektron wirkt: F q vec E pq.N Aufgrund dieser Kraft wird das Elektron beschleunigt: a fracFm pq.eq Mit dieser Beschleunigung muss das Elektron eine halbe Seitenlänge also fracs nach oben zurücklegen; damit kann die Zeit bestimmt werden zu welcher das Elektron wieder aus dem Würfel austritt: t sqrtfracsa pq.s Schliesslich berechnen wir s_x: s_x v t pq.m itemb Wenn die Magnetfeldrichtung nach unten zeigt so wird das Elektron aufgrund der Lorentzkraft auf eine Kreisbahn gelenkt; mit der Dreifingerregel findet man die Richtung des Kreises. Das Elektron wird den Würfel durch das Quadrat ABFE verlassen Achtung: Elektron negativ geladen vec F qvec v times vec B. Die Kreisbahn auf welcher sich das Elektron bewegen wird hat den folgen Radius: r fracmvqB pq.m enumerate
Contained in these collections:

