Gedämpfte schwingende Boje
About points...
We associate a certain number of points with each exercise.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
About difficulty...
We associate a certain difficulty with each exercise.
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
Question
Solution
Short
Video
\(\LaTeX\)

Need help? Yes, please!
The following quantities appear in the problem:
The following formulas must be used to solve the exercise:
No explanation / solution video to this exercise has yet been created.
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Exercise:
Eine Zylinderboje mit Radius r und Masse m ruht im Wasser. Sie werde hat y ins Wasser Dichte sscrhoW gedrückt. abclist abc Zeige dass diese Zylinderboje bei Vernachlässigung der Dämpfung harmonisch mit der Kreisfrequenz al omega_ sqrtfracsscrhoW g pim r schwingt. hfill Hinweis: Es ist textbfkeine detaillierte Lösung der DGL verlangt sondern lediglich ein Reduzieren der Bewegungsgleichung in die Form at -omega_^ yt. abc Berechne die Masse einer solchen Zylinderboje mit ro Radius wenn sie mit fo schwingt. hfill abclist In der Realität stellt man fest dass bereits nach t die Amplitude bloss noch eto der anfänglichen Amplitude beträgt. Nimm an dass die gedämpfte Schwingung über die Positionsfunktion al yt hat y qty-delta t cosomega t beschrieben werden kann. abclist setcounterabc setcounterenumii abc Berechne den Dämpfungsparameter delta. hfill abc Skizziere im folgen Diagramm die Auslenkung des gedämpften Systems in Abhängigkeit der Zeit für eine Anfangsamplitude von mm. Gehe davon aus dass das gedämpfte System die gleiche Schwingungsdauer wie das ungedämpfte System hat. hfill abc Was passiert nach knapp .s? hfill abclist center tikzpicture tkzInitxmin xmax ymin- ymax tkzGridsub subystep. subxstep. tkzDrawXright labelt/sis tkzDrawYabove labely/simm tkzTextbelowsmall. tkzTextbelowsmall. tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tikzpicture center
Solution:
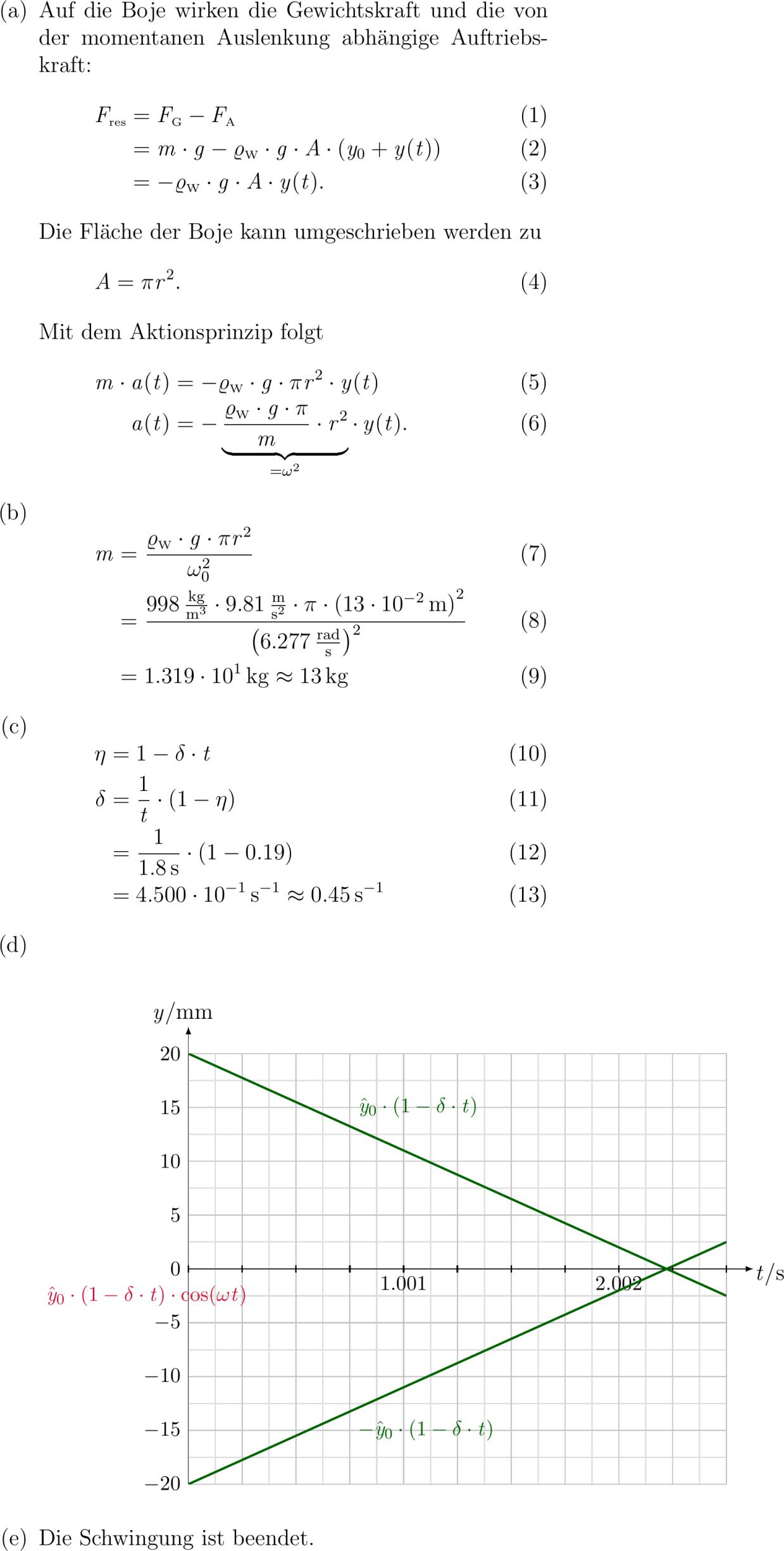
abclist abc Auf die Boje wirken die Gewichtskraft und die von der momentanen Auslenkung abhängige Auftriebskraft: al sscFres sscFG - sscFA m g - sscrhoW g A y_ + yt - sscrhoW g A yt. Die Fläche der Boje kann umgeschrieben werden zu al A pi r^. Mit dem Aktionsprinzip folgt al m at -sscrhoW g pi r^ yt at -underbracefracsscrhoW g pim r^_omega^ yt. abc al m mf fracRW ncg pi qtyr^qtyfC^ m approx mTT abc al eta -delta t delta Df fract qty-et D approx DTT abc phantom. center tikzpicture tkzInitxmin xmax ymin- ymax tkzGridsub subystep. subxstep. tkzDrawXright labelt/sis tkzDrawYabove labely/simm tkzTextbelowsmall. tkzTextbelowsmall. tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzFctvery thick darkgreen domain:*-./*x tkzDefPoByFct tkzTextabove right darkgreentkzPoResultsmallhat y_ qty-delta t tkzTextleft darkred.-.smallhat y_ qty-delta t cosomega t tkzFctvery thick darkgreen-*-./*x tkzDefPoByFct tkzTextbelow right darkgreentkzPoResultsmall-hat y_ qty-delta t tkzFctvery thick darkred domain:*-./*x*cosdeg.*x tikzpicture center abc Die Schwingung ist beet. abclist
Eine Zylinderboje mit Radius r und Masse m ruht im Wasser. Sie werde hat y ins Wasser Dichte sscrhoW gedrückt. abclist abc Zeige dass diese Zylinderboje bei Vernachlässigung der Dämpfung harmonisch mit der Kreisfrequenz al omega_ sqrtfracsscrhoW g pim r schwingt. hfill Hinweis: Es ist textbfkeine detaillierte Lösung der DGL verlangt sondern lediglich ein Reduzieren der Bewegungsgleichung in die Form at -omega_^ yt. abc Berechne die Masse einer solchen Zylinderboje mit ro Radius wenn sie mit fo schwingt. hfill abclist In der Realität stellt man fest dass bereits nach t die Amplitude bloss noch eto der anfänglichen Amplitude beträgt. Nimm an dass die gedämpfte Schwingung über die Positionsfunktion al yt hat y qty-delta t cosomega t beschrieben werden kann. abclist setcounterabc setcounterenumii abc Berechne den Dämpfungsparameter delta. hfill abc Skizziere im folgen Diagramm die Auslenkung des gedämpften Systems in Abhängigkeit der Zeit für eine Anfangsamplitude von mm. Gehe davon aus dass das gedämpfte System die gleiche Schwingungsdauer wie das ungedämpfte System hat. hfill abc Was passiert nach knapp .s? hfill abclist center tikzpicture tkzInitxmin xmax ymin- ymax tkzGridsub subystep. subxstep. tkzDrawXright labelt/sis tkzDrawYabove labely/simm tkzTextbelowsmall. tkzTextbelowsmall. tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tikzpicture center
Solution:
abclist abc Auf die Boje wirken die Gewichtskraft und die von der momentanen Auslenkung abhängige Auftriebskraft: al sscFres sscFG - sscFA m g - sscrhoW g A y_ + yt - sscrhoW g A yt. Die Fläche der Boje kann umgeschrieben werden zu al A pi r^. Mit dem Aktionsprinzip folgt al m at -sscrhoW g pi r^ yt at -underbracefracsscrhoW g pim r^_omega^ yt. abc al m mf fracRW ncg pi qtyr^qtyfC^ m approx mTT abc al eta -delta t delta Df fract qty-et D approx DTT abc phantom. center tikzpicture tkzInitxmin xmax ymin- ymax tkzGridsub subystep. subxstep. tkzDrawXright labelt/sis tkzDrawYabove labely/simm tkzTextbelowsmall. tkzTextbelowsmall. tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzFctvery thick darkgreen domain:*-./*x tkzDefPoByFct tkzTextabove right darkgreentkzPoResultsmallhat y_ qty-delta t tkzTextleft darkred.-.smallhat y_ qty-delta t cosomega t tkzFctvery thick darkgreen-*-./*x tkzDefPoByFct tkzTextbelow right darkgreentkzPoResultsmall-hat y_ qty-delta t tkzFctvery thick darkred domain:*-./*x*cosdeg.*x tikzpicture center abc Die Schwingung ist beet. abclist
Meta Information
Exercise:
Eine Zylinderboje mit Radius r und Masse m ruht im Wasser. Sie werde hat y ins Wasser Dichte sscrhoW gedrückt. abclist abc Zeige dass diese Zylinderboje bei Vernachlässigung der Dämpfung harmonisch mit der Kreisfrequenz al omega_ sqrtfracsscrhoW g pim r schwingt. hfill Hinweis: Es ist textbfkeine detaillierte Lösung der DGL verlangt sondern lediglich ein Reduzieren der Bewegungsgleichung in die Form at -omega_^ yt. abc Berechne die Masse einer solchen Zylinderboje mit ro Radius wenn sie mit fo schwingt. hfill abclist In der Realität stellt man fest dass bereits nach t die Amplitude bloss noch eto der anfänglichen Amplitude beträgt. Nimm an dass die gedämpfte Schwingung über die Positionsfunktion al yt hat y qty-delta t cosomega t beschrieben werden kann. abclist setcounterabc setcounterenumii abc Berechne den Dämpfungsparameter delta. hfill abc Skizziere im folgen Diagramm die Auslenkung des gedämpften Systems in Abhängigkeit der Zeit für eine Anfangsamplitude von mm. Gehe davon aus dass das gedämpfte System die gleiche Schwingungsdauer wie das ungedämpfte System hat. hfill abc Was passiert nach knapp .s? hfill abclist center tikzpicture tkzInitxmin xmax ymin- ymax tkzGridsub subystep. subxstep. tkzDrawXright labelt/sis tkzDrawYabove labely/simm tkzTextbelowsmall. tkzTextbelowsmall. tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tikzpicture center
Solution:
abclist abc Auf die Boje wirken die Gewichtskraft und die von der momentanen Auslenkung abhängige Auftriebskraft: al sscFres sscFG - sscFA m g - sscrhoW g A y_ + yt - sscrhoW g A yt. Die Fläche der Boje kann umgeschrieben werden zu al A pi r^. Mit dem Aktionsprinzip folgt al m at -sscrhoW g pi r^ yt at -underbracefracsscrhoW g pim r^_omega^ yt. abc al m mf fracRW ncg pi qtyr^qtyfC^ m approx mTT abc al eta -delta t delta Df fract qty-et D approx DTT abc phantom. center tikzpicture tkzInitxmin xmax ymin- ymax tkzGridsub subystep. subxstep. tkzDrawXright labelt/sis tkzDrawYabove labely/simm tkzTextbelowsmall. tkzTextbelowsmall. tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzFctvery thick darkgreen domain:*-./*x tkzDefPoByFct tkzTextabove right darkgreentkzPoResultsmallhat y_ qty-delta t tkzTextleft darkred.-.smallhat y_ qty-delta t cosomega t tkzFctvery thick darkgreen-*-./*x tkzDefPoByFct tkzTextbelow right darkgreentkzPoResultsmall-hat y_ qty-delta t tkzFctvery thick darkred domain:*-./*x*cosdeg.*x tikzpicture center abc Die Schwingung ist beet. abclist
Eine Zylinderboje mit Radius r und Masse m ruht im Wasser. Sie werde hat y ins Wasser Dichte sscrhoW gedrückt. abclist abc Zeige dass diese Zylinderboje bei Vernachlässigung der Dämpfung harmonisch mit der Kreisfrequenz al omega_ sqrtfracsscrhoW g pim r schwingt. hfill Hinweis: Es ist textbfkeine detaillierte Lösung der DGL verlangt sondern lediglich ein Reduzieren der Bewegungsgleichung in die Form at -omega_^ yt. abc Berechne die Masse einer solchen Zylinderboje mit ro Radius wenn sie mit fo schwingt. hfill abclist In der Realität stellt man fest dass bereits nach t die Amplitude bloss noch eto der anfänglichen Amplitude beträgt. Nimm an dass die gedämpfte Schwingung über die Positionsfunktion al yt hat y qty-delta t cosomega t beschrieben werden kann. abclist setcounterabc setcounterenumii abc Berechne den Dämpfungsparameter delta. hfill abc Skizziere im folgen Diagramm die Auslenkung des gedämpften Systems in Abhängigkeit der Zeit für eine Anfangsamplitude von mm. Gehe davon aus dass das gedämpfte System die gleiche Schwingungsdauer wie das ungedämpfte System hat. hfill abc Was passiert nach knapp .s? hfill abclist center tikzpicture tkzInitxmin xmax ymin- ymax tkzGridsub subystep. subxstep. tkzDrawXright labelt/sis tkzDrawYabove labely/simm tkzTextbelowsmall. tkzTextbelowsmall. tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tikzpicture center
Solution:
abclist abc Auf die Boje wirken die Gewichtskraft und die von der momentanen Auslenkung abhängige Auftriebskraft: al sscFres sscFG - sscFA m g - sscrhoW g A y_ + yt - sscrhoW g A yt. Die Fläche der Boje kann umgeschrieben werden zu al A pi r^. Mit dem Aktionsprinzip folgt al m at -sscrhoW g pi r^ yt at -underbracefracsscrhoW g pim r^_omega^ yt. abc al m mf fracRW ncg pi qtyr^qtyfC^ m approx mTT abc al eta -delta t delta Df fract qty-et D approx DTT abc phantom. center tikzpicture tkzInitxmin xmax ymin- ymax tkzGridsub subystep. subxstep. tkzDrawXright labelt/sis tkzDrawYabove labely/simm tkzTextbelowsmall. tkzTextbelowsmall. tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzTextleft-small- tkzTextleftsmall tkzFctvery thick darkgreen domain:*-./*x tkzDefPoByFct tkzTextabove right darkgreentkzPoResultsmallhat y_ qty-delta t tkzTextleft darkred.-.smallhat y_ qty-delta t cosomega t tkzFctvery thick darkgreen-*-./*x tkzDefPoByFct tkzTextbelow right darkgreentkzPoResultsmall-hat y_ qty-delta t tkzFctvery thick darkred domain:*-./*x*cosdeg.*x tikzpicture center abc Die Schwingung ist beet. abclist
Contained in these collections:
-
Gedämpfte Schwingung by TeXercises

