Geladene Kugel in einer Röhre
About points...
We associate a certain number of points with each exercise.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
About difficulty...
We associate a certain difficulty with each exercise.
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
Question
Solution
Short
Video
\(\LaTeX\)

No explanation / solution video to this exercise has yet been created.
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Exercise:
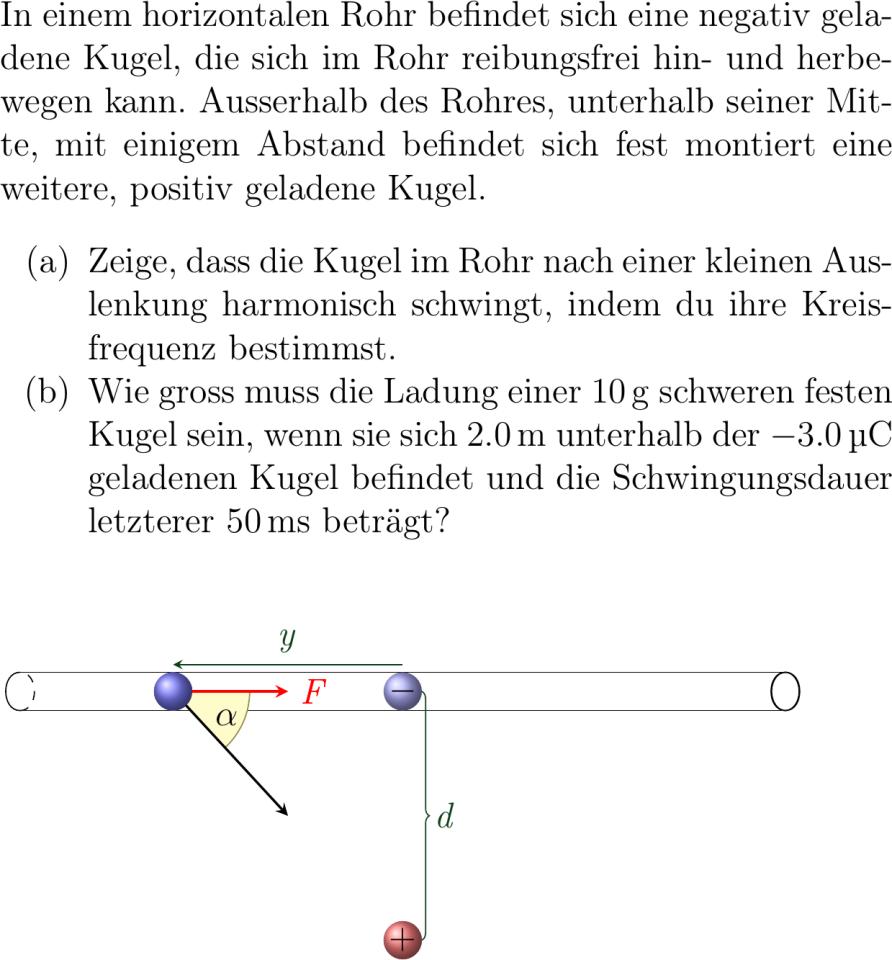
In einem horizontalen Rohr befindet sich eine negativ geladene Kugel die sich im Rohr reibungsfrei hin- und herbewegen kann. Ausserhalb des Rohres unterhalb seiner Mitte mit einigem Abstand befindet sich fest montiert eine weitere positiv geladene Kugel. abclist abc Zeige dass die Kugel im Rohr nach einer kleinen Auslenkung harmonisch schwingt indem du ihre Kreisfrequenz bestimmst. abc Wie gross muss die Ladung einer g schweren festen Kugel sein wenn sie sich .m unterhalb der -.microcoulomb geladenen Kugel befindet und die Schwingungsdauer letzterer ms beträgt? abclist center tikzpicturescale.stealth drawwhite .-- .; draw --; draw .--.; draw . ellipse . and .; draw .. controls -. and -.. .. .; drawdashed .. controls . and .. .. .; draw .. controls . and .. .. .; draw .. controls . and .. .. .; shadeball colorblue!!white . circle .; shadeball colorred!!white - circle .; node at - +; node at . -; drawsnakebrace colorgreen!!black . .--.- noderight midway d; shadeball colorblue!!white . circle .; shadeball colorred!!white - circle .; node at - +; node at . -; drawcolorgreen!!black- stealth .--. nodemidway above y; shadeball colorblue!!white . circle .; node at . -; %node at .- F_mboxscriptsizeelekt-kfracq_q_r^; draw- thick red .--.. noderight F; % angle: . degrees shadeball colorblue!!white . circle .; node at . -; filldrawfillyellow!drawyellow!!black . -- . arc :-.: -- cycle; node at . -. alpha; draw- thick red .--.. noderight F; % angle: . degrees draw- thick . -- +. -.;% nodebelow F_mboxscriptsizeelekt; % length: . shadeball colorblue!!white . circle .; %node at . -; %nodered at . - FF_mboxscriptsizeelekt cosalpha; %node at . -. cosalphafracyr; %node at . -. F -k fracq_q_y^+d^ fracysqrty^+d^; tikzpicture center
Solution:
abclist abc Die Frage ist nun ob sich die blaue Kugel wenn sie aus ihrer Ruhelage ausgelenkt wird harmonisch schwingt. Die die Kugel rücktreibe Kraft ist die elektrische Anziehungskraft zwischen den beiden verschieden geladenen Kugeln. Die blaue Kugel erfährt dabei eine in der Skizze schwarz eingezeichnete Kraft in Richtung der roten Kugel mit der Stärke sscFE fracpiepsilon_ fracq_q_r^ fracpiepsilon_ fracq_q_d^+y^ wobei r^ d^+y^ der Abstand der beiden Kugeln ist. Der Kraftanteil der die blaue Kugel nun zurück zur Ruhelage bringt in der Skizze als roter Pfeil eingezeichnet ist: F -sscFE cosalpha -sscFE fracyr -sscFE fracysqrtd^+y^ -fracpiepsilon_ fracq_q_d^+y^ fracysqrtd^+y^ -fracpiepsilon_ fracq_q_d^+y^^frac y Egal wie man diesen letzten Ausdruck nun algebraisch umstellt man wird ihn nicht auf die Form F-Ky bringen. Es handelt sich hierbei also streng genommen nicht um eine harmonische Schwingung. Schaut man allerdings nur kleine Auslenkungen y an geme ist yll d so gilt y^+d^^frac approx d^^frac d^ und die rücktreibe Kraft wird zu: sscFres -fracpiepsilon_ fracq_q_d^+y^^frac y -fracq_q_piepsilon_ d^ y. Mit dem Aktionsprinzip folgt schliesslich al m at -fracq_q_piepsilon_ d^ yt at -underbracefracq_q_pi m epsilon_ d^_omega^ yt. Die Kreisfrequenz der Schwingung ist damit al omega sqrtfracq_q_pi m epsilon_ d^. labelkugelosz abc newqtyd.m newqtyqz.C newqtyTs newqtymkg Wir lösen den Ausdruck refkugelosz nach der einen Ladung auf solqtyqefracpi^ mepsilon_ d^q_T^*pi***mn*ncepsn*dn**/qzn*Tn**C al q_ fracpi m omega^ epsilon_ d^q_ qef fracpi^mncepsqtyd^qzqtyT^ qe qeII abclist
In einem horizontalen Rohr befindet sich eine negativ geladene Kugel die sich im Rohr reibungsfrei hin- und herbewegen kann. Ausserhalb des Rohres unterhalb seiner Mitte mit einigem Abstand befindet sich fest montiert eine weitere positiv geladene Kugel. abclist abc Zeige dass die Kugel im Rohr nach einer kleinen Auslenkung harmonisch schwingt indem du ihre Kreisfrequenz bestimmst. abc Wie gross muss die Ladung einer g schweren festen Kugel sein wenn sie sich .m unterhalb der -.microcoulomb geladenen Kugel befindet und die Schwingungsdauer letzterer ms beträgt? abclist center tikzpicturescale.stealth drawwhite .-- .; draw --; draw .--.; draw . ellipse . and .; draw .. controls -. and -.. .. .; drawdashed .. controls . and .. .. .; draw .. controls . and .. .. .; draw .. controls . and .. .. .; shadeball colorblue!!white . circle .; shadeball colorred!!white - circle .; node at - +; node at . -; drawsnakebrace colorgreen!!black . .--.- noderight midway d; shadeball colorblue!!white . circle .; shadeball colorred!!white - circle .; node at - +; node at . -; drawcolorgreen!!black- stealth .--. nodemidway above y; shadeball colorblue!!white . circle .; node at . -; %node at .- F_mboxscriptsizeelekt-kfracq_q_r^; draw- thick red .--.. noderight F; % angle: . degrees shadeball colorblue!!white . circle .; node at . -; filldrawfillyellow!drawyellow!!black . -- . arc :-.: -- cycle; node at . -. alpha; draw- thick red .--.. noderight F; % angle: . degrees draw- thick . -- +. -.;% nodebelow F_mboxscriptsizeelekt; % length: . shadeball colorblue!!white . circle .; %node at . -; %nodered at . - FF_mboxscriptsizeelekt cosalpha; %node at . -. cosalphafracyr; %node at . -. F -k fracq_q_y^+d^ fracysqrty^+d^; tikzpicture center
Solution:
abclist abc Die Frage ist nun ob sich die blaue Kugel wenn sie aus ihrer Ruhelage ausgelenkt wird harmonisch schwingt. Die die Kugel rücktreibe Kraft ist die elektrische Anziehungskraft zwischen den beiden verschieden geladenen Kugeln. Die blaue Kugel erfährt dabei eine in der Skizze schwarz eingezeichnete Kraft in Richtung der roten Kugel mit der Stärke sscFE fracpiepsilon_ fracq_q_r^ fracpiepsilon_ fracq_q_d^+y^ wobei r^ d^+y^ der Abstand der beiden Kugeln ist. Der Kraftanteil der die blaue Kugel nun zurück zur Ruhelage bringt in der Skizze als roter Pfeil eingezeichnet ist: F -sscFE cosalpha -sscFE fracyr -sscFE fracysqrtd^+y^ -fracpiepsilon_ fracq_q_d^+y^ fracysqrtd^+y^ -fracpiepsilon_ fracq_q_d^+y^^frac y Egal wie man diesen letzten Ausdruck nun algebraisch umstellt man wird ihn nicht auf die Form F-Ky bringen. Es handelt sich hierbei also streng genommen nicht um eine harmonische Schwingung. Schaut man allerdings nur kleine Auslenkungen y an geme ist yll d so gilt y^+d^^frac approx d^^frac d^ und die rücktreibe Kraft wird zu: sscFres -fracpiepsilon_ fracq_q_d^+y^^frac y -fracq_q_piepsilon_ d^ y. Mit dem Aktionsprinzip folgt schliesslich al m at -fracq_q_piepsilon_ d^ yt at -underbracefracq_q_pi m epsilon_ d^_omega^ yt. Die Kreisfrequenz der Schwingung ist damit al omega sqrtfracq_q_pi m epsilon_ d^. labelkugelosz abc newqtyd.m newqtyqz.C newqtyTs newqtymkg Wir lösen den Ausdruck refkugelosz nach der einen Ladung auf solqtyqefracpi^ mepsilon_ d^q_T^*pi***mn*ncepsn*dn**/qzn*Tn**C al q_ fracpi m omega^ epsilon_ d^q_ qef fracpi^mncepsqtyd^qzqtyT^ qe qeII abclist
Meta Information
Exercise:
In einem horizontalen Rohr befindet sich eine negativ geladene Kugel die sich im Rohr reibungsfrei hin- und herbewegen kann. Ausserhalb des Rohres unterhalb seiner Mitte mit einigem Abstand befindet sich fest montiert eine weitere positiv geladene Kugel. abclist abc Zeige dass die Kugel im Rohr nach einer kleinen Auslenkung harmonisch schwingt indem du ihre Kreisfrequenz bestimmst. abc Wie gross muss die Ladung einer g schweren festen Kugel sein wenn sie sich .m unterhalb der -.microcoulomb geladenen Kugel befindet und die Schwingungsdauer letzterer ms beträgt? abclist center tikzpicturescale.stealth drawwhite .-- .; draw --; draw .--.; draw . ellipse . and .; draw .. controls -. and -.. .. .; drawdashed .. controls . and .. .. .; draw .. controls . and .. .. .; draw .. controls . and .. .. .; shadeball colorblue!!white . circle .; shadeball colorred!!white - circle .; node at - +; node at . -; drawsnakebrace colorgreen!!black . .--.- noderight midway d; shadeball colorblue!!white . circle .; shadeball colorred!!white - circle .; node at - +; node at . -; drawcolorgreen!!black- stealth .--. nodemidway above y; shadeball colorblue!!white . circle .; node at . -; %node at .- F_mboxscriptsizeelekt-kfracq_q_r^; draw- thick red .--.. noderight F; % angle: . degrees shadeball colorblue!!white . circle .; node at . -; filldrawfillyellow!drawyellow!!black . -- . arc :-.: -- cycle; node at . -. alpha; draw- thick red .--.. noderight F; % angle: . degrees draw- thick . -- +. -.;% nodebelow F_mboxscriptsizeelekt; % length: . shadeball colorblue!!white . circle .; %node at . -; %nodered at . - FF_mboxscriptsizeelekt cosalpha; %node at . -. cosalphafracyr; %node at . -. F -k fracq_q_y^+d^ fracysqrty^+d^; tikzpicture center
Solution:
abclist abc Die Frage ist nun ob sich die blaue Kugel wenn sie aus ihrer Ruhelage ausgelenkt wird harmonisch schwingt. Die die Kugel rücktreibe Kraft ist die elektrische Anziehungskraft zwischen den beiden verschieden geladenen Kugeln. Die blaue Kugel erfährt dabei eine in der Skizze schwarz eingezeichnete Kraft in Richtung der roten Kugel mit der Stärke sscFE fracpiepsilon_ fracq_q_r^ fracpiepsilon_ fracq_q_d^+y^ wobei r^ d^+y^ der Abstand der beiden Kugeln ist. Der Kraftanteil der die blaue Kugel nun zurück zur Ruhelage bringt in der Skizze als roter Pfeil eingezeichnet ist: F -sscFE cosalpha -sscFE fracyr -sscFE fracysqrtd^+y^ -fracpiepsilon_ fracq_q_d^+y^ fracysqrtd^+y^ -fracpiepsilon_ fracq_q_d^+y^^frac y Egal wie man diesen letzten Ausdruck nun algebraisch umstellt man wird ihn nicht auf die Form F-Ky bringen. Es handelt sich hierbei also streng genommen nicht um eine harmonische Schwingung. Schaut man allerdings nur kleine Auslenkungen y an geme ist yll d so gilt y^+d^^frac approx d^^frac d^ und die rücktreibe Kraft wird zu: sscFres -fracpiepsilon_ fracq_q_d^+y^^frac y -fracq_q_piepsilon_ d^ y. Mit dem Aktionsprinzip folgt schliesslich al m at -fracq_q_piepsilon_ d^ yt at -underbracefracq_q_pi m epsilon_ d^_omega^ yt. Die Kreisfrequenz der Schwingung ist damit al omega sqrtfracq_q_pi m epsilon_ d^. labelkugelosz abc newqtyd.m newqtyqz.C newqtyTs newqtymkg Wir lösen den Ausdruck refkugelosz nach der einen Ladung auf solqtyqefracpi^ mepsilon_ d^q_T^*pi***mn*ncepsn*dn**/qzn*Tn**C al q_ fracpi m omega^ epsilon_ d^q_ qef fracpi^mncepsqtyd^qzqtyT^ qe qeII abclist
In einem horizontalen Rohr befindet sich eine negativ geladene Kugel die sich im Rohr reibungsfrei hin- und herbewegen kann. Ausserhalb des Rohres unterhalb seiner Mitte mit einigem Abstand befindet sich fest montiert eine weitere positiv geladene Kugel. abclist abc Zeige dass die Kugel im Rohr nach einer kleinen Auslenkung harmonisch schwingt indem du ihre Kreisfrequenz bestimmst. abc Wie gross muss die Ladung einer g schweren festen Kugel sein wenn sie sich .m unterhalb der -.microcoulomb geladenen Kugel befindet und die Schwingungsdauer letzterer ms beträgt? abclist center tikzpicturescale.stealth drawwhite .-- .; draw --; draw .--.; draw . ellipse . and .; draw .. controls -. and -.. .. .; drawdashed .. controls . and .. .. .; draw .. controls . and .. .. .; draw .. controls . and .. .. .; shadeball colorblue!!white . circle .; shadeball colorred!!white - circle .; node at - +; node at . -; drawsnakebrace colorgreen!!black . .--.- noderight midway d; shadeball colorblue!!white . circle .; shadeball colorred!!white - circle .; node at - +; node at . -; drawcolorgreen!!black- stealth .--. nodemidway above y; shadeball colorblue!!white . circle .; node at . -; %node at .- F_mboxscriptsizeelekt-kfracq_q_r^; draw- thick red .--.. noderight F; % angle: . degrees shadeball colorblue!!white . circle .; node at . -; filldrawfillyellow!drawyellow!!black . -- . arc :-.: -- cycle; node at . -. alpha; draw- thick red .--.. noderight F; % angle: . degrees draw- thick . -- +. -.;% nodebelow F_mboxscriptsizeelekt; % length: . shadeball colorblue!!white . circle .; %node at . -; %nodered at . - FF_mboxscriptsizeelekt cosalpha; %node at . -. cosalphafracyr; %node at . -. F -k fracq_q_y^+d^ fracysqrty^+d^; tikzpicture center
Solution:
abclist abc Die Frage ist nun ob sich die blaue Kugel wenn sie aus ihrer Ruhelage ausgelenkt wird harmonisch schwingt. Die die Kugel rücktreibe Kraft ist die elektrische Anziehungskraft zwischen den beiden verschieden geladenen Kugeln. Die blaue Kugel erfährt dabei eine in der Skizze schwarz eingezeichnete Kraft in Richtung der roten Kugel mit der Stärke sscFE fracpiepsilon_ fracq_q_r^ fracpiepsilon_ fracq_q_d^+y^ wobei r^ d^+y^ der Abstand der beiden Kugeln ist. Der Kraftanteil der die blaue Kugel nun zurück zur Ruhelage bringt in der Skizze als roter Pfeil eingezeichnet ist: F -sscFE cosalpha -sscFE fracyr -sscFE fracysqrtd^+y^ -fracpiepsilon_ fracq_q_d^+y^ fracysqrtd^+y^ -fracpiepsilon_ fracq_q_d^+y^^frac y Egal wie man diesen letzten Ausdruck nun algebraisch umstellt man wird ihn nicht auf die Form F-Ky bringen. Es handelt sich hierbei also streng genommen nicht um eine harmonische Schwingung. Schaut man allerdings nur kleine Auslenkungen y an geme ist yll d so gilt y^+d^^frac approx d^^frac d^ und die rücktreibe Kraft wird zu: sscFres -fracpiepsilon_ fracq_q_d^+y^^frac y -fracq_q_piepsilon_ d^ y. Mit dem Aktionsprinzip folgt schliesslich al m at -fracq_q_piepsilon_ d^ yt at -underbracefracq_q_pi m epsilon_ d^_omega^ yt. Die Kreisfrequenz der Schwingung ist damit al omega sqrtfracq_q_pi m epsilon_ d^. labelkugelosz abc newqtyd.m newqtyqz.C newqtyTs newqtymkg Wir lösen den Ausdruck refkugelosz nach der einen Ladung auf solqtyqefracpi^ mepsilon_ d^q_T^*pi***mn*ncepsn*dn**/qzn*Tn**C al q_ fracpi m omega^ epsilon_ d^q_ qef fracpi^mncepsqtyd^qzqtyT^ qe qeII abclist
Contained in these collections:
-
-
Harmonische Schwingung: Geladene Kugel by TeXercises

