Surface of an ice floe with a man on it
About points...
We associate a certain number of points with each exercise.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
About difficulty...
We associate a certain difficulty with each exercise.
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
Question
Solution
Short
Video
\(\LaTeX\)

Need help? Yes, please!
The following quantities appear in the problem:
Länge \(\ell\) / Masse \(m\) / Kraft \(F\) / Volumen \(V\) / Ortsfaktor \(g\) / Höhe \(h\) / Dichte \(\varrho\) / Breite \(b\) /
The following formulas must be used to solve the exercise:
\(F = \varrho V g \quad \) \(F = mg \quad \) \(V = abc \quad \)

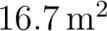
Exercise:
A d thick ice floe rE floats in the North Sea which is frozen over in places. What area would it have to have at least to be able to carry a man of with mM mass?
Solution:
newqtyd.m newqtyr.ekgpcm newqtymkg % The weight of the man and the ice floe together must correspond exactly to the buoyancy force. AuftriebSchritte PGleichungsscFGE + sscFGM sscFA PGleichungsscmE g + sscmM g sscrhoFl g sscVver PGleichungsscrhoE Ad g + sscmMg sscrhoFl g Ad AlgebraSchritte MGleichungsscrhoFl g Ad - sscrhoE Ad g sscmMg MGleichungsscrhoFl-sscrhoEAdg sscmM g MGleichungA fracsscmMsscrhoFl-sscrhoEd PHYSMATH % This means that the ice floe must have an area of at least: newqtyskgpcm solqtyAfracsscmMsscrhoFl-sscrhoEdmn/sn-rn/dnsquaremeter al A Af fracmqtys-r d A TecA
A d thick ice floe rE floats in the North Sea which is frozen over in places. What area would it have to have at least to be able to carry a man of with mM mass?
Solution:
newqtyd.m newqtyr.ekgpcm newqtymkg % The weight of the man and the ice floe together must correspond exactly to the buoyancy force. AuftriebSchritte PGleichungsscFGE + sscFGM sscFA PGleichungsscmE g + sscmM g sscrhoFl g sscVver PGleichungsscrhoE Ad g + sscmMg sscrhoFl g Ad AlgebraSchritte MGleichungsscrhoFl g Ad - sscrhoE Ad g sscmMg MGleichungsscrhoFl-sscrhoEAdg sscmM g MGleichungA fracsscmMsscrhoFl-sscrhoEd PHYSMATH % This means that the ice floe must have an area of at least: newqtyskgpcm solqtyAfracsscmMsscrhoFl-sscrhoEdmn/sn-rn/dnsquaremeter al A Af fracmqtys-r d A TecA
Meta Information
Exercise:
A d thick ice floe rE floats in the North Sea which is frozen over in places. What area would it have to have at least to be able to carry a man of with mM mass?
Solution:
newqtyd.m newqtyr.ekgpcm newqtymkg % The weight of the man and the ice floe together must correspond exactly to the buoyancy force. AuftriebSchritte PGleichungsscFGE + sscFGM sscFA PGleichungsscmE g + sscmM g sscrhoFl g sscVver PGleichungsscrhoE Ad g + sscmMg sscrhoFl g Ad AlgebraSchritte MGleichungsscrhoFl g Ad - sscrhoE Ad g sscmMg MGleichungsscrhoFl-sscrhoEAdg sscmM g MGleichungA fracsscmMsscrhoFl-sscrhoEd PHYSMATH % This means that the ice floe must have an area of at least: newqtyskgpcm solqtyAfracsscmMsscrhoFl-sscrhoEdmn/sn-rn/dnsquaremeter al A Af fracmqtys-r d A TecA
A d thick ice floe rE floats in the North Sea which is frozen over in places. What area would it have to have at least to be able to carry a man of with mM mass?
Solution:
newqtyd.m newqtyr.ekgpcm newqtymkg % The weight of the man and the ice floe together must correspond exactly to the buoyancy force. AuftriebSchritte PGleichungsscFGE + sscFGM sscFA PGleichungsscmE g + sscmM g sscrhoFl g sscVver PGleichungsscrhoE Ad g + sscmMg sscrhoFl g Ad AlgebraSchritte MGleichungsscrhoFl g Ad - sscrhoE Ad g sscmMg MGleichungsscrhoFl-sscrhoEAdg sscmM g MGleichungA fracsscmMsscrhoFl-sscrhoEd PHYSMATH % This means that the ice floe must have an area of at least: newqtyskgpcm solqtyAfracsscmMsscrhoFl-sscrhoEdmn/sn-rn/dnsquaremeter al A Af fracmqtys-r d A TecA
Contained in these collections:
-
Floss oder Eisscholle by TeXercises
-
Auftrieb 2 by uz
Asked Quantity:
Fläche \(A\)
in
Quadratmeter \(\rm m^2\)
Physical Quantity
Flächeninhalt
2-dimensionale Teilmenge des 3-dimensionalen Raumes
Unit
Quadratmeter (\(\rm m^2\))
Base?
SI?
Metric?
Coherent?
Imperial?
\(\rm45\,m^2\): Wohnfläche
\(\rm1\,m^2\): DIN A0
\(\rm41285\,km^2\): Schweiz
\(\rm400\,m^2\): Darm
\(\rm670\,m^2\): Tennis-Court