Zwei Kreise
Question
Solution
Short
Video
\(\LaTeX\)
Need help? Yes, please!
The following quantities appear in the problem:
Drehmoment \(\vec M\) /
The following formulas must be used to solve the exercise:
\(\sum \stackrel{\curvearrowleft}{M} \stackrel{!}{=} \sum \stackrel{\curvearrowright}{M} \quad \)
No explanation / solution video to this exercise has yet been created.
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Exercise:
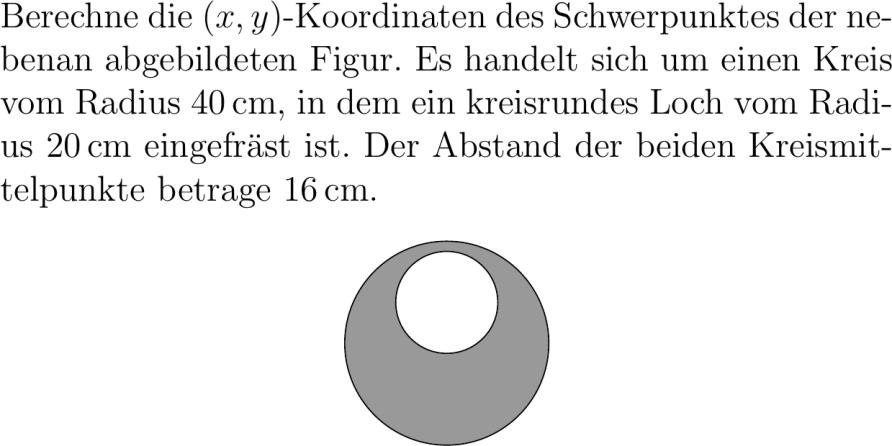
Berechne die xy-Koordinaten des Schwerpunktes der nebenan abgebildeten Figur. Es handelt sich um einen Kreis vom Radius pqcm in dem ein kreisrundes Loch vom Radius pqcm eingefräst ist. Der Abstand der beiden Kreismittelpunkte betrage pqcm. center tikzpicturescale. filldrawfillblack!!white circle cm; filldrawfillwhite . circle cm; tikzpicture center
Solution:
Es gelte folges Koordinatensystem: center tikzpicturescale. latex filldrawfillblack!!white circle cm; filldrawfillwhite . circle cm; draw- colorgreen!!black -.---.- noderight x; draw- colorgreen!!black -.--. nodeabove y; filldrawcolorblack fillyellow -. circle .cm; tikzpicture center Es ist einsichtig dass die x-Koordinate des Schwerpunkts sein muss da die Figur bezüglich y-Achse spiegelsymmetrisch ist. Der weisse Punkt auf der negativen y-Achse zeigt eine Vermutung für den Ort des Schwerpunkts an. Die y-Achse wird dann so gewählt dass die y-Koordinate in diesem System gerade auch ist. Nur nützt das einem natürlich nicht viel. Man sollte wissen wo im Kreis das der Fall ist. Dazu muss man angeben wie weit dieser Punkt vom Mittelpunkt des grossen oder kleinen Kreises weg ist. In unserem Koordinatensystem gilt folge Gleichung: y F_g + +y -F_k mustbe Darin ist F_g die Gewichtskraft des vollen grossen Kreises und F_k die Gewichtskraft der kleinen Kreises wenn er voll wäre. D.h. man betrachtet das Loch als Kreis negativer Masse auf einem grossen Kreis positiver Masse. Die Massen der Kreise sind proportional zu ihrer Fläche deshalb gilt y pi r_g^ - +y pi r_k^ &mustbe y - +y y . Alternative Lösung mit Schwerpunktformel: Aus Symmetriegründen muss die x-Koordinate des Schwerpunkts gerade sein. Für die y-Koordinate finden wir mit der Schwerpunktformel newqtyrecm newqtyrzcm newqtydcm solqtyy-fracr_^dr_^-r_^-rzn***dn/ren**-rzn**cm al y^* fracm_y_+m_y_m_+m_ fracr_^y_-r_^y_r_^-r_^ yf -fracqtyrz^ dqtyre^-qtyrz^ yTTT. Wir haben dabei benutzt dass die Masse überall proportional zur Fläche und damit zum Quadrat des Radius' ist d.h. m_i c r_i^. Ausserdem muss die Masse des Lochs subtrahiert werden deshalb das negative Vorzeichen.
Berechne die xy-Koordinaten des Schwerpunktes der nebenan abgebildeten Figur. Es handelt sich um einen Kreis vom Radius pqcm in dem ein kreisrundes Loch vom Radius pqcm eingefräst ist. Der Abstand der beiden Kreismittelpunkte betrage pqcm. center tikzpicturescale. filldrawfillblack!!white circle cm; filldrawfillwhite . circle cm; tikzpicture center
Solution:
Es gelte folges Koordinatensystem: center tikzpicturescale. latex filldrawfillblack!!white circle cm; filldrawfillwhite . circle cm; draw- colorgreen!!black -.---.- noderight x; draw- colorgreen!!black -.--. nodeabove y; filldrawcolorblack fillyellow -. circle .cm; tikzpicture center Es ist einsichtig dass die x-Koordinate des Schwerpunkts sein muss da die Figur bezüglich y-Achse spiegelsymmetrisch ist. Der weisse Punkt auf der negativen y-Achse zeigt eine Vermutung für den Ort des Schwerpunkts an. Die y-Achse wird dann so gewählt dass die y-Koordinate in diesem System gerade auch ist. Nur nützt das einem natürlich nicht viel. Man sollte wissen wo im Kreis das der Fall ist. Dazu muss man angeben wie weit dieser Punkt vom Mittelpunkt des grossen oder kleinen Kreises weg ist. In unserem Koordinatensystem gilt folge Gleichung: y F_g + +y -F_k mustbe Darin ist F_g die Gewichtskraft des vollen grossen Kreises und F_k die Gewichtskraft der kleinen Kreises wenn er voll wäre. D.h. man betrachtet das Loch als Kreis negativer Masse auf einem grossen Kreis positiver Masse. Die Massen der Kreise sind proportional zu ihrer Fläche deshalb gilt y pi r_g^ - +y pi r_k^ &mustbe y - +y y . Alternative Lösung mit Schwerpunktformel: Aus Symmetriegründen muss die x-Koordinate des Schwerpunkts gerade sein. Für die y-Koordinate finden wir mit der Schwerpunktformel newqtyrecm newqtyrzcm newqtydcm solqtyy-fracr_^dr_^-r_^-rzn***dn/ren**-rzn**cm al y^* fracm_y_+m_y_m_+m_ fracr_^y_-r_^y_r_^-r_^ yf -fracqtyrz^ dqtyre^-qtyrz^ yTTT. Wir haben dabei benutzt dass die Masse überall proportional zur Fläche und damit zum Quadrat des Radius' ist d.h. m_i c r_i^. Ausserdem muss die Masse des Lochs subtrahiert werden deshalb das negative Vorzeichen.