Äquivalentdosis aufgrund von Kalium
About points...
We associate a certain number of points with each exercise.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
About difficulty...
We associate a certain difficulty with each exercise.
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
Question
Solution
Short
Video
\(\LaTeX\)

Need help? Yes, please!
The following quantities appear in the problem:
The following formulas must be used to solve the exercise:

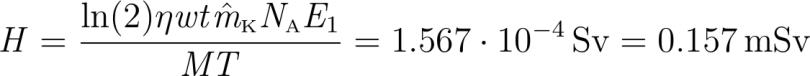
No explanation / solution video to this exercise has yet been created.
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Exercise:
Der menschlichen Körper mMO enthält rund .g Kalium pro Kilogramm Körpermasse. Kalium spielt beim SäurBasHaushalt von Zellen eine wichtige Rolle und kommt in der Natur als Isotopengemisch aus isotopeK isotopeK isotopeK vor. Die Isotope isotopeK und isotopeK sind stabil. Die isotopeK-Kerne zerfallen durch upbeta-Zerfall Qualitätsfaktor mit TO Halbwertszeit und haben netO Anteil am Isotopengemisch. Die emittierten Elektronen haben durchschnittlich EeO Energie. Welche Äquivalentdosis nimmt der Körper wegen des Kaliums währ eines Jahres auf? Gehe davon aus dass die Bewegungsenergie der emittierten upbeta-Teilchen vollständig vom Körper absorbiert wird.
Solution:
Im menschlichen Körper befinden sich tilde m sscmM sschat mK mM ne mT Kalium wovon m eta tilde m eta sscmM sschat mK net mT mK Kalium- sind was rund n fracmM fraceta sscmM sschat mKM fracmKMK n N fraceta sscmM sschat mKM sscNA N isotopeK-Atomen entspricht. Diese haben A lambda N fracln T N fracln Tfraceta sscmMsschat mKM sscNA lam N fracln T N A Aktivität welche sich währ eines Jahres aufgrund der hohen Halbwertszeit und weil auch ständig neues Kalium nachgefüllt wird kaum verändert. Es werden also währ einem Jahr N_a A t fracln Tfraceta sscmMsschat mKM sscNA t A t Na Strahlen ausgesandt was einer total absorbierten Energie von E N_a E_ fract ln Tfraceta sscmMsschat mK sscNAM E_ Na Ee E entspricht. Über den ganzen Körper verteilt ist das D fracEsscmM fract ln Tfraceta sscmMsschat mK sscNA sscmM M E_ fracEmM D Energiedosis und H wD w fract ln Tfraceta sschat mK sscNA M E_ w D H HP- Äquivalentdosis. H fracln eta wt sschat mK sscNA E_ M T H HP-
Der menschlichen Körper mMO enthält rund .g Kalium pro Kilogramm Körpermasse. Kalium spielt beim SäurBasHaushalt von Zellen eine wichtige Rolle und kommt in der Natur als Isotopengemisch aus isotopeK isotopeK isotopeK vor. Die Isotope isotopeK und isotopeK sind stabil. Die isotopeK-Kerne zerfallen durch upbeta-Zerfall Qualitätsfaktor mit TO Halbwertszeit und haben netO Anteil am Isotopengemisch. Die emittierten Elektronen haben durchschnittlich EeO Energie. Welche Äquivalentdosis nimmt der Körper wegen des Kaliums währ eines Jahres auf? Gehe davon aus dass die Bewegungsenergie der emittierten upbeta-Teilchen vollständig vom Körper absorbiert wird.
Solution:
Im menschlichen Körper befinden sich tilde m sscmM sschat mK mM ne mT Kalium wovon m eta tilde m eta sscmM sschat mK net mT mK Kalium- sind was rund n fracmM fraceta sscmM sschat mKM fracmKMK n N fraceta sscmM sschat mKM sscNA N isotopeK-Atomen entspricht. Diese haben A lambda N fracln T N fracln Tfraceta sscmMsschat mKM sscNA lam N fracln T N A Aktivität welche sich währ eines Jahres aufgrund der hohen Halbwertszeit und weil auch ständig neues Kalium nachgefüllt wird kaum verändert. Es werden also währ einem Jahr N_a A t fracln Tfraceta sscmMsschat mKM sscNA t A t Na Strahlen ausgesandt was einer total absorbierten Energie von E N_a E_ fract ln Tfraceta sscmMsschat mK sscNAM E_ Na Ee E entspricht. Über den ganzen Körper verteilt ist das D fracEsscmM fract ln Tfraceta sscmMsschat mK sscNA sscmM M E_ fracEmM D Energiedosis und H wD w fract ln Tfraceta sschat mK sscNA M E_ w D H HP- Äquivalentdosis. H fracln eta wt sschat mK sscNA E_ M T H HP-
Meta Information
Exercise:
Der menschlichen Körper mMO enthält rund .g Kalium pro Kilogramm Körpermasse. Kalium spielt beim SäurBasHaushalt von Zellen eine wichtige Rolle und kommt in der Natur als Isotopengemisch aus isotopeK isotopeK isotopeK vor. Die Isotope isotopeK und isotopeK sind stabil. Die isotopeK-Kerne zerfallen durch upbeta-Zerfall Qualitätsfaktor mit TO Halbwertszeit und haben netO Anteil am Isotopengemisch. Die emittierten Elektronen haben durchschnittlich EeO Energie. Welche Äquivalentdosis nimmt der Körper wegen des Kaliums währ eines Jahres auf? Gehe davon aus dass die Bewegungsenergie der emittierten upbeta-Teilchen vollständig vom Körper absorbiert wird.
Solution:
Im menschlichen Körper befinden sich tilde m sscmM sschat mK mM ne mT Kalium wovon m eta tilde m eta sscmM sschat mK net mT mK Kalium- sind was rund n fracmM fraceta sscmM sschat mKM fracmKMK n N fraceta sscmM sschat mKM sscNA N isotopeK-Atomen entspricht. Diese haben A lambda N fracln T N fracln Tfraceta sscmMsschat mKM sscNA lam N fracln T N A Aktivität welche sich währ eines Jahres aufgrund der hohen Halbwertszeit und weil auch ständig neues Kalium nachgefüllt wird kaum verändert. Es werden also währ einem Jahr N_a A t fracln Tfraceta sscmMsschat mKM sscNA t A t Na Strahlen ausgesandt was einer total absorbierten Energie von E N_a E_ fract ln Tfraceta sscmMsschat mK sscNAM E_ Na Ee E entspricht. Über den ganzen Körper verteilt ist das D fracEsscmM fract ln Tfraceta sscmMsschat mK sscNA sscmM M E_ fracEmM D Energiedosis und H wD w fract ln Tfraceta sschat mK sscNA M E_ w D H HP- Äquivalentdosis. H fracln eta wt sschat mK sscNA E_ M T H HP-
Der menschlichen Körper mMO enthält rund .g Kalium pro Kilogramm Körpermasse. Kalium spielt beim SäurBasHaushalt von Zellen eine wichtige Rolle und kommt in der Natur als Isotopengemisch aus isotopeK isotopeK isotopeK vor. Die Isotope isotopeK und isotopeK sind stabil. Die isotopeK-Kerne zerfallen durch upbeta-Zerfall Qualitätsfaktor mit TO Halbwertszeit und haben netO Anteil am Isotopengemisch. Die emittierten Elektronen haben durchschnittlich EeO Energie. Welche Äquivalentdosis nimmt der Körper wegen des Kaliums währ eines Jahres auf? Gehe davon aus dass die Bewegungsenergie der emittierten upbeta-Teilchen vollständig vom Körper absorbiert wird.
Solution:
Im menschlichen Körper befinden sich tilde m sscmM sschat mK mM ne mT Kalium wovon m eta tilde m eta sscmM sschat mK net mT mK Kalium- sind was rund n fracmM fraceta sscmM sschat mKM fracmKMK n N fraceta sscmM sschat mKM sscNA N isotopeK-Atomen entspricht. Diese haben A lambda N fracln T N fracln Tfraceta sscmMsschat mKM sscNA lam N fracln T N A Aktivität welche sich währ eines Jahres aufgrund der hohen Halbwertszeit und weil auch ständig neues Kalium nachgefüllt wird kaum verändert. Es werden also währ einem Jahr N_a A t fracln Tfraceta sscmMsschat mKM sscNA t A t Na Strahlen ausgesandt was einer total absorbierten Energie von E N_a E_ fract ln Tfraceta sscmMsschat mK sscNAM E_ Na Ee E entspricht. Über den ganzen Körper verteilt ist das D fracEsscmM fract ln Tfraceta sscmMsschat mK sscNA sscmM M E_ fracEmM D Energiedosis und H wD w fract ln Tfraceta sschat mK sscNA M E_ w D H HP- Äquivalentdosis. H fracln eta wt sschat mK sscNA E_ M T H HP-
Contained in these collections:
-
Dosimetrie 2 by uz
-
Körperdosis aufgrund von ... by TeXercises
Asked Quantity:
Organdosis \(H\)
in
Sievert \(\rm Sv\)
Physical Quantity
Äquivalentdosis
im Körper angerichteter Schaden, empirisch
\(H = w_{\rm R} \cdot D\)
Unit
Sievert (\(\rm Sv\))
Base?
SI?
Metric?
Coherent?
Imperial?

