Baggerarbeit
About points...
We associate a certain number of points with each exercise.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
About difficulty...
We associate a certain difficulty with each exercise.
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
Question
Solution
Short
Video
\(\LaTeX\)

No explanation / solution video to this exercise has yet been created.
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Exercise:
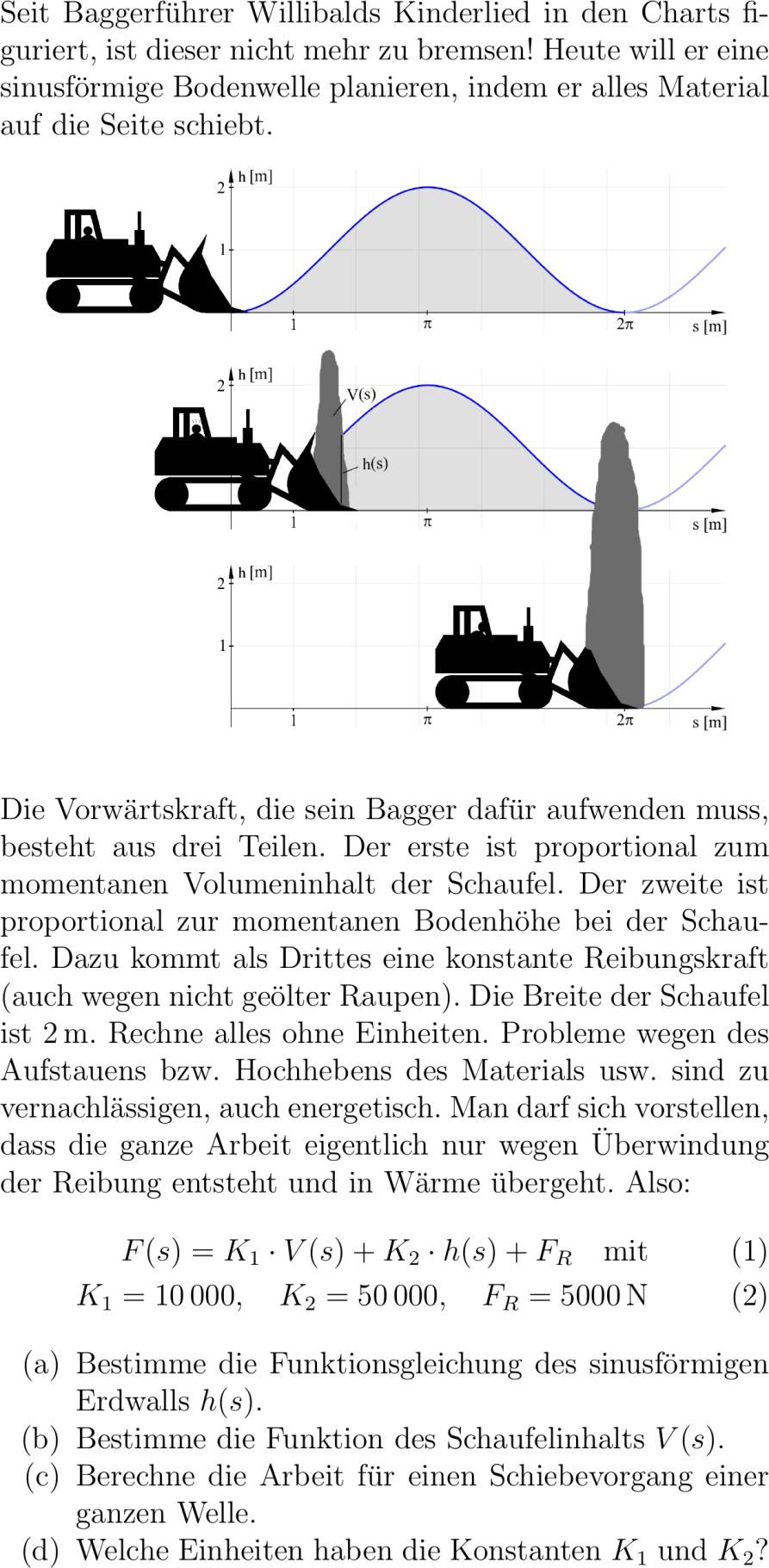
Seit Baggerführer Willibalds Kinderlied in den Charts figuriert ist dieser nicht mehr zu bremsen! Heute will er eine sinusförmige Bodenwelle planieren indem er alles Material auf die Seite schiebt. center includegraphicswidth.textwidth#image_path:baggerarbeit# center Die Vorwärtskraft die sein Bagger dafür aufwen muss besteht aus drei Teilen. Der erste ist proportional zum momentanen Volumeninhalt der Schaufel. Der zweite ist proportional zur momentanen Bodenhöhe bei der Schaufel. Dazu kommt als Drittes eine konstante Reibungskraft auch wegen nicht geölter Raupen. Die Breite der Schaufel ist m. Rechne alles ohne Einheiten. Probleme wegen des Aufstauens bzw. Hochhebens des Materials usw. sind zu vernachlässigen auch energetisch. Man darf sich vorstellen dass die ganze Arbeit eigentlich nur wegen Überwindung der Reibung entsteht und in Wärme übergeht. Also: Fs K_ Vs + K_ hs + F_Rquadmboxmit K_numprquad K_ numprquad F_R N abcliste abc Bestimme die Funktionsgleichung des sinusförmigen Erdwalls hs. abc Bestimme die Funktion des Schaufelinhalts Vs. abc Berechne die Arbeit für einen Schiebevorgang einer ganzen Welle. abc Welche Einheiten haben die Konstanten K_ und K_? abcliste
Solution:
abcliste abc Laut Aufgabe ist die Bodenwelle sinusförmig. Man kann auf einen Blick sehen dass der Sinus nach oben verschoben ist d.h. die x-Achse müsste bei ypqm angebracht werden um einen glqq normalengrqq Verlauf zu erhalten. Damit ist einsichtig dass die Höhe durch hs -cos s ausgedrückt werden kann. abc Der Schaufelinhalt ein Volumen kann aus der Schaufelbreite und der glqq Flächegrqq des Schaufeinhaltes von der Seite gesehen berechnet werden: Vs _^s A htilde s mboxdtilde s _^s -cos tilde s mboxd tilde s s-sin s. abc Um eine ganze Welle zu schieben von dots pi wie aus der Grafik ersichtlich ist die Arbeit W Fsmboxd s _^pi leftK_ Vs + K_ hs + F_Rrightmboxds _^pi leftnumpre s-sin s +numpre -cos s + numprerightmboxds numpre leftfracs^+cos sright_^pi + numpre lefts-sin sright_^pi + numpreleftsright_^pi numprepi^ + numpr.epi pq.eJ. abc Damit eine Kraft Einheit Newton entsteht müssen die Einheiten der Konstanten K_ fractextkgtexts^textm^ K_ fractextkgtexts^ sein. abcliste
Seit Baggerführer Willibalds Kinderlied in den Charts figuriert ist dieser nicht mehr zu bremsen! Heute will er eine sinusförmige Bodenwelle planieren indem er alles Material auf die Seite schiebt. center includegraphicswidth.textwidth#image_path:baggerarbeit# center Die Vorwärtskraft die sein Bagger dafür aufwen muss besteht aus drei Teilen. Der erste ist proportional zum momentanen Volumeninhalt der Schaufel. Der zweite ist proportional zur momentanen Bodenhöhe bei der Schaufel. Dazu kommt als Drittes eine konstante Reibungskraft auch wegen nicht geölter Raupen. Die Breite der Schaufel ist m. Rechne alles ohne Einheiten. Probleme wegen des Aufstauens bzw. Hochhebens des Materials usw. sind zu vernachlässigen auch energetisch. Man darf sich vorstellen dass die ganze Arbeit eigentlich nur wegen Überwindung der Reibung entsteht und in Wärme übergeht. Also: Fs K_ Vs + K_ hs + F_Rquadmboxmit K_numprquad K_ numprquad F_R N abcliste abc Bestimme die Funktionsgleichung des sinusförmigen Erdwalls hs. abc Bestimme die Funktion des Schaufelinhalts Vs. abc Berechne die Arbeit für einen Schiebevorgang einer ganzen Welle. abc Welche Einheiten haben die Konstanten K_ und K_? abcliste
Solution:
abcliste abc Laut Aufgabe ist die Bodenwelle sinusförmig. Man kann auf einen Blick sehen dass der Sinus nach oben verschoben ist d.h. die x-Achse müsste bei ypqm angebracht werden um einen glqq normalengrqq Verlauf zu erhalten. Damit ist einsichtig dass die Höhe durch hs -cos s ausgedrückt werden kann. abc Der Schaufelinhalt ein Volumen kann aus der Schaufelbreite und der glqq Flächegrqq des Schaufeinhaltes von der Seite gesehen berechnet werden: Vs _^s A htilde s mboxdtilde s _^s -cos tilde s mboxd tilde s s-sin s. abc Um eine ganze Welle zu schieben von dots pi wie aus der Grafik ersichtlich ist die Arbeit W Fsmboxd s _^pi leftK_ Vs + K_ hs + F_Rrightmboxds _^pi leftnumpre s-sin s +numpre -cos s + numprerightmboxds numpre leftfracs^+cos sright_^pi + numpre lefts-sin sright_^pi + numpreleftsright_^pi numprepi^ + numpr.epi pq.eJ. abc Damit eine Kraft Einheit Newton entsteht müssen die Einheiten der Konstanten K_ fractextkgtexts^textm^ K_ fractextkgtexts^ sein. abcliste
Meta Information
Exercise:
Seit Baggerführer Willibalds Kinderlied in den Charts figuriert ist dieser nicht mehr zu bremsen! Heute will er eine sinusförmige Bodenwelle planieren indem er alles Material auf die Seite schiebt. center includegraphicswidth.textwidth#image_path:baggerarbeit# center Die Vorwärtskraft die sein Bagger dafür aufwen muss besteht aus drei Teilen. Der erste ist proportional zum momentanen Volumeninhalt der Schaufel. Der zweite ist proportional zur momentanen Bodenhöhe bei der Schaufel. Dazu kommt als Drittes eine konstante Reibungskraft auch wegen nicht geölter Raupen. Die Breite der Schaufel ist m. Rechne alles ohne Einheiten. Probleme wegen des Aufstauens bzw. Hochhebens des Materials usw. sind zu vernachlässigen auch energetisch. Man darf sich vorstellen dass die ganze Arbeit eigentlich nur wegen Überwindung der Reibung entsteht und in Wärme übergeht. Also: Fs K_ Vs + K_ hs + F_Rquadmboxmit K_numprquad K_ numprquad F_R N abcliste abc Bestimme die Funktionsgleichung des sinusförmigen Erdwalls hs. abc Bestimme die Funktion des Schaufelinhalts Vs. abc Berechne die Arbeit für einen Schiebevorgang einer ganzen Welle. abc Welche Einheiten haben die Konstanten K_ und K_? abcliste
Solution:
abcliste abc Laut Aufgabe ist die Bodenwelle sinusförmig. Man kann auf einen Blick sehen dass der Sinus nach oben verschoben ist d.h. die x-Achse müsste bei ypqm angebracht werden um einen glqq normalengrqq Verlauf zu erhalten. Damit ist einsichtig dass die Höhe durch hs -cos s ausgedrückt werden kann. abc Der Schaufelinhalt ein Volumen kann aus der Schaufelbreite und der glqq Flächegrqq des Schaufeinhaltes von der Seite gesehen berechnet werden: Vs _^s A htilde s mboxdtilde s _^s -cos tilde s mboxd tilde s s-sin s. abc Um eine ganze Welle zu schieben von dots pi wie aus der Grafik ersichtlich ist die Arbeit W Fsmboxd s _^pi leftK_ Vs + K_ hs + F_Rrightmboxds _^pi leftnumpre s-sin s +numpre -cos s + numprerightmboxds numpre leftfracs^+cos sright_^pi + numpre lefts-sin sright_^pi + numpreleftsright_^pi numprepi^ + numpr.epi pq.eJ. abc Damit eine Kraft Einheit Newton entsteht müssen die Einheiten der Konstanten K_ fractextkgtexts^textm^ K_ fractextkgtexts^ sein. abcliste
Seit Baggerführer Willibalds Kinderlied in den Charts figuriert ist dieser nicht mehr zu bremsen! Heute will er eine sinusförmige Bodenwelle planieren indem er alles Material auf die Seite schiebt. center includegraphicswidth.textwidth#image_path:baggerarbeit# center Die Vorwärtskraft die sein Bagger dafür aufwen muss besteht aus drei Teilen. Der erste ist proportional zum momentanen Volumeninhalt der Schaufel. Der zweite ist proportional zur momentanen Bodenhöhe bei der Schaufel. Dazu kommt als Drittes eine konstante Reibungskraft auch wegen nicht geölter Raupen. Die Breite der Schaufel ist m. Rechne alles ohne Einheiten. Probleme wegen des Aufstauens bzw. Hochhebens des Materials usw. sind zu vernachlässigen auch energetisch. Man darf sich vorstellen dass die ganze Arbeit eigentlich nur wegen Überwindung der Reibung entsteht und in Wärme übergeht. Also: Fs K_ Vs + K_ hs + F_Rquadmboxmit K_numprquad K_ numprquad F_R N abcliste abc Bestimme die Funktionsgleichung des sinusförmigen Erdwalls hs. abc Bestimme die Funktion des Schaufelinhalts Vs. abc Berechne die Arbeit für einen Schiebevorgang einer ganzen Welle. abc Welche Einheiten haben die Konstanten K_ und K_? abcliste
Solution:
abcliste abc Laut Aufgabe ist die Bodenwelle sinusförmig. Man kann auf einen Blick sehen dass der Sinus nach oben verschoben ist d.h. die x-Achse müsste bei ypqm angebracht werden um einen glqq normalengrqq Verlauf zu erhalten. Damit ist einsichtig dass die Höhe durch hs -cos s ausgedrückt werden kann. abc Der Schaufelinhalt ein Volumen kann aus der Schaufelbreite und der glqq Flächegrqq des Schaufeinhaltes von der Seite gesehen berechnet werden: Vs _^s A htilde s mboxdtilde s _^s -cos tilde s mboxd tilde s s-sin s. abc Um eine ganze Welle zu schieben von dots pi wie aus der Grafik ersichtlich ist die Arbeit W Fsmboxd s _^pi leftK_ Vs + K_ hs + F_Rrightmboxds _^pi leftnumpre s-sin s +numpre -cos s + numprerightmboxds numpre leftfracs^+cos sright_^pi + numpre lefts-sin sright_^pi + numpreleftsright_^pi numprepi^ + numpr.epi pq.eJ. abc Damit eine Kraft Einheit Newton entsteht müssen die Einheiten der Konstanten K_ fractextkgtexts^textm^ K_ fractextkgtexts^ sein. abcliste
Contained in these collections:
-
PAM Matura 2007 Stans by uz

