Experiment zur Längenausdehnung
About points...
We associate a certain number of points with each exercise.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
About difficulty...
We associate a certain difficulty with each exercise.
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
Question
Solution
Short
Video
\(\LaTeX\)


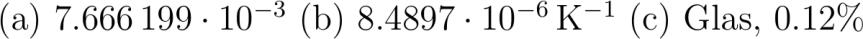
No explanation / solution video to this exercise has yet been created.
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Exercise:
Im Labor wird ein pq.cm langer Stab aus unbekanntem Material erwärmt. In der folgen Tabelle sind die bei bestimmter Temperatur gemessenen Längenveränderungen aufgeführt. center tabularx.textwidth|l||X|X|X|X|X|X|X| hline leftthetarightCelsius & & & & & & & hline leftDelta lrightmboxmm & & . & . & . & . & . & . hline tabularx center abcliste abc Berechne mittels textttLIN REG des textttTI-+ die lineare Funktion Delta l k Delta theta. D.h. gib die Funktion textttY_ an. Die Berechnung von aus eizelnen Werten in der Tabelle gibt keinen Punkt! Es müssen mittels Regression alle Werte in die Berechnung einbezogen werden. abc Berechne den Ausdehnungskoeffizienten dieses Materials. Die Berechnung des Koeffizienten aus einzelnen Werten in der Tabelle gibt keinen Punkt! abc Stelle aufgrund eines Vergleiches mit einer Tabelle eine Vermutung an um welches Material es sich handeln könnte und berechne dann die prozentuale Abweichung des experimentellen Wertes vom Referenzwert in der Tabelle. abcliste
Solution:
abcliste abc Eine lineare Regression durch die Messdaten liefert als beste Gerade die Funktion Y numpr. X - numpr. Ein Vergleich mit Delta l k Deltatheta erlaubt es die Konstante k direkt abzulesen leftkright numpr.. abc Die Konstante k ist laut Theorie k l_ alpha quadmboxalso alpha frackl_ fracpq.m/Kpq.m pq.K^-. abc Ein Vergleich mit dem Formelbuch Fundamentum zeigt dass es sich um Glas handeln könnte. Die prozentuale Abweichung vom dort angegebenen Wert ist -fracpq.K^-pq.K^- . .%. Anmerkung: Dieser Vergleich ist allerdings wenig sinnvoll da der Tabellenwert nur auf zwei signifikante Stellen angegeben ist. abcliste
Im Labor wird ein pq.cm langer Stab aus unbekanntem Material erwärmt. In der folgen Tabelle sind die bei bestimmter Temperatur gemessenen Längenveränderungen aufgeführt. center tabularx.textwidth|l||X|X|X|X|X|X|X| hline leftthetarightCelsius & & & & & & & hline leftDelta lrightmboxmm & & . & . & . & . & . & . hline tabularx center abcliste abc Berechne mittels textttLIN REG des textttTI-+ die lineare Funktion Delta l k Delta theta. D.h. gib die Funktion textttY_ an. Die Berechnung von aus eizelnen Werten in der Tabelle gibt keinen Punkt! Es müssen mittels Regression alle Werte in die Berechnung einbezogen werden. abc Berechne den Ausdehnungskoeffizienten dieses Materials. Die Berechnung des Koeffizienten aus einzelnen Werten in der Tabelle gibt keinen Punkt! abc Stelle aufgrund eines Vergleiches mit einer Tabelle eine Vermutung an um welches Material es sich handeln könnte und berechne dann die prozentuale Abweichung des experimentellen Wertes vom Referenzwert in der Tabelle. abcliste
Solution:
abcliste abc Eine lineare Regression durch die Messdaten liefert als beste Gerade die Funktion Y numpr. X - numpr. Ein Vergleich mit Delta l k Deltatheta erlaubt es die Konstante k direkt abzulesen leftkright numpr.. abc Die Konstante k ist laut Theorie k l_ alpha quadmboxalso alpha frackl_ fracpq.m/Kpq.m pq.K^-. abc Ein Vergleich mit dem Formelbuch Fundamentum zeigt dass es sich um Glas handeln könnte. Die prozentuale Abweichung vom dort angegebenen Wert ist -fracpq.K^-pq.K^- . .%. Anmerkung: Dieser Vergleich ist allerdings wenig sinnvoll da der Tabellenwert nur auf zwei signifikante Stellen angegeben ist. abcliste
Meta Information
Exercise:
Im Labor wird ein pq.cm langer Stab aus unbekanntem Material erwärmt. In der folgen Tabelle sind die bei bestimmter Temperatur gemessenen Längenveränderungen aufgeführt. center tabularx.textwidth|l||X|X|X|X|X|X|X| hline leftthetarightCelsius & & & & & & & hline leftDelta lrightmboxmm & & . & . & . & . & . & . hline tabularx center abcliste abc Berechne mittels textttLIN REG des textttTI-+ die lineare Funktion Delta l k Delta theta. D.h. gib die Funktion textttY_ an. Die Berechnung von aus eizelnen Werten in der Tabelle gibt keinen Punkt! Es müssen mittels Regression alle Werte in die Berechnung einbezogen werden. abc Berechne den Ausdehnungskoeffizienten dieses Materials. Die Berechnung des Koeffizienten aus einzelnen Werten in der Tabelle gibt keinen Punkt! abc Stelle aufgrund eines Vergleiches mit einer Tabelle eine Vermutung an um welches Material es sich handeln könnte und berechne dann die prozentuale Abweichung des experimentellen Wertes vom Referenzwert in der Tabelle. abcliste
Solution:
abcliste abc Eine lineare Regression durch die Messdaten liefert als beste Gerade die Funktion Y numpr. X - numpr. Ein Vergleich mit Delta l k Deltatheta erlaubt es die Konstante k direkt abzulesen leftkright numpr.. abc Die Konstante k ist laut Theorie k l_ alpha quadmboxalso alpha frackl_ fracpq.m/Kpq.m pq.K^-. abc Ein Vergleich mit dem Formelbuch Fundamentum zeigt dass es sich um Glas handeln könnte. Die prozentuale Abweichung vom dort angegebenen Wert ist -fracpq.K^-pq.K^- . .%. Anmerkung: Dieser Vergleich ist allerdings wenig sinnvoll da der Tabellenwert nur auf zwei signifikante Stellen angegeben ist. abcliste
Im Labor wird ein pq.cm langer Stab aus unbekanntem Material erwärmt. In der folgen Tabelle sind die bei bestimmter Temperatur gemessenen Längenveränderungen aufgeführt. center tabularx.textwidth|l||X|X|X|X|X|X|X| hline leftthetarightCelsius & & & & & & & hline leftDelta lrightmboxmm & & . & . & . & . & . & . hline tabularx center abcliste abc Berechne mittels textttLIN REG des textttTI-+ die lineare Funktion Delta l k Delta theta. D.h. gib die Funktion textttY_ an. Die Berechnung von aus eizelnen Werten in der Tabelle gibt keinen Punkt! Es müssen mittels Regression alle Werte in die Berechnung einbezogen werden. abc Berechne den Ausdehnungskoeffizienten dieses Materials. Die Berechnung des Koeffizienten aus einzelnen Werten in der Tabelle gibt keinen Punkt! abc Stelle aufgrund eines Vergleiches mit einer Tabelle eine Vermutung an um welches Material es sich handeln könnte und berechne dann die prozentuale Abweichung des experimentellen Wertes vom Referenzwert in der Tabelle. abcliste
Solution:
abcliste abc Eine lineare Regression durch die Messdaten liefert als beste Gerade die Funktion Y numpr. X - numpr. Ein Vergleich mit Delta l k Deltatheta erlaubt es die Konstante k direkt abzulesen leftkright numpr.. abc Die Konstante k ist laut Theorie k l_ alpha quadmboxalso alpha frackl_ fracpq.m/Kpq.m pq.K^-. abc Ein Vergleich mit dem Formelbuch Fundamentum zeigt dass es sich um Glas handeln könnte. Die prozentuale Abweichung vom dort angegebenen Wert ist -fracpq.K^-pq.K^- . .%. Anmerkung: Dieser Vergleich ist allerdings wenig sinnvoll da der Tabellenwert nur auf zwei signifikante Stellen angegeben ist. abcliste
Contained in these collections:
-
-
Ausdehnungskoeffizient bestimmen by TeXercises

