Reaktionszeit
About points...
We associate a certain number of points with each exercise.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
About difficulty...
We associate a certain difficulty with each exercise.
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
Question
Solution
Short
Video
\(\LaTeX\)

Need help? Yes, please!
The following quantities appear in the problem:
Zeit \(t\) / Geschwindigkeit \(v\) / Strecke \(s\) / Beschleunigung \(a\) /
The following formulas must be used to solve the exercise:
\(v = v_0 + at \quad \) \(s = \dfrac{1}{2}at^2+v_0 t \quad \) \(s = \dfrac{v^2-v_0^2}{2a} \quad \) \(s = vt \quad \)

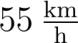
Exercise:
Ein Auto fährt mit kilometerperhour. Plötzlich taucht in m Entfernung ein Hindernis auf und der Fahrer führt eine Vollbremsung durch. Die Reaktionszeit des Fahrers beträgt eine Sekunde d.h. die Zeit verstreicht vom Erkennen des Hindernisses bis zum Einleiten des Bremsvorgangs. Das Auto kommt genau vor dem Hindernis zum Stehen. Nun kommt das gleiche Auto mit kilometerperhour in dieselbe Situation. Mit welcher Gschwin-dig-keit prallt es auf das Hindernis?
Solution:
In der Reaktionszeit die der Fahrer braucht bis er dann auch lich bremst legt er noch eine Strecke von s_textscriptsize R vt labelreaktionsweg meterpersecond s m labelhindernisabstand zurück. Auf den übrigen m bremst er dann das Auto mit Vollbremsung -- also der bestmöglichen negativen Beschleunigung -- von kilometerperhour auf null ab. Damit finden wir a fracv^s fracleftmeterpersecondright^ m .meterpersecondsquared. So effektiv kann dieses Auto also abbremsen. Wenn es nun mit kilometerperhour in dieselbe Situation kommt so legt es bis der Fahrer anfängt zu Bremsen schon m zurück: s'_textscriptsize R vt meterpersecond s m Bleiben also nur noch m bis zum Hindernis! Die Zeit welche verstreicht bis das Auto am Hindernis ankommt führt auf eine quadratische Gleichung: s fracat^+v_t fracat^ +v_ t -s underbracefrac-.meterpersecondsquared_A t^ underbrace+meterpersecond_B underbracm_C Diese quadratische Gleichung hat die beiden Lösungen t .s t' .s Nur die erste Lösung ist physikalisch sinnvoll. Die Geschwindigkeit welche das Auto am Hindernis noch hat ist somit: v at+v_ -at+v_ labelbremsbeschl -.meterpersecondsquared .s+meterpersecond .meterpersecond approx kilometerperhour Der Wagen trifft also mit einer Geschwindigkeit von rund kilometerperhour auf das Hindernis!
Ein Auto fährt mit kilometerperhour. Plötzlich taucht in m Entfernung ein Hindernis auf und der Fahrer führt eine Vollbremsung durch. Die Reaktionszeit des Fahrers beträgt eine Sekunde d.h. die Zeit verstreicht vom Erkennen des Hindernisses bis zum Einleiten des Bremsvorgangs. Das Auto kommt genau vor dem Hindernis zum Stehen. Nun kommt das gleiche Auto mit kilometerperhour in dieselbe Situation. Mit welcher Gschwin-dig-keit prallt es auf das Hindernis?
Solution:
In der Reaktionszeit die der Fahrer braucht bis er dann auch lich bremst legt er noch eine Strecke von s_textscriptsize R vt labelreaktionsweg meterpersecond s m labelhindernisabstand zurück. Auf den übrigen m bremst er dann das Auto mit Vollbremsung -- also der bestmöglichen negativen Beschleunigung -- von kilometerperhour auf null ab. Damit finden wir a fracv^s fracleftmeterpersecondright^ m .meterpersecondsquared. So effektiv kann dieses Auto also abbremsen. Wenn es nun mit kilometerperhour in dieselbe Situation kommt so legt es bis der Fahrer anfängt zu Bremsen schon m zurück: s'_textscriptsize R vt meterpersecond s m Bleiben also nur noch m bis zum Hindernis! Die Zeit welche verstreicht bis das Auto am Hindernis ankommt führt auf eine quadratische Gleichung: s fracat^+v_t fracat^ +v_ t -s underbracefrac-.meterpersecondsquared_A t^ underbrace+meterpersecond_B underbracm_C Diese quadratische Gleichung hat die beiden Lösungen t .s t' .s Nur die erste Lösung ist physikalisch sinnvoll. Die Geschwindigkeit welche das Auto am Hindernis noch hat ist somit: v at+v_ -at+v_ labelbremsbeschl -.meterpersecondsquared .s+meterpersecond .meterpersecond approx kilometerperhour Der Wagen trifft also mit einer Geschwindigkeit von rund kilometerperhour auf das Hindernis!
Meta Information
Exercise:
Ein Auto fährt mit kilometerperhour. Plötzlich taucht in m Entfernung ein Hindernis auf und der Fahrer führt eine Vollbremsung durch. Die Reaktionszeit des Fahrers beträgt eine Sekunde d.h. die Zeit verstreicht vom Erkennen des Hindernisses bis zum Einleiten des Bremsvorgangs. Das Auto kommt genau vor dem Hindernis zum Stehen. Nun kommt das gleiche Auto mit kilometerperhour in dieselbe Situation. Mit welcher Gschwin-dig-keit prallt es auf das Hindernis?
Solution:
In der Reaktionszeit die der Fahrer braucht bis er dann auch lich bremst legt er noch eine Strecke von s_textscriptsize R vt labelreaktionsweg meterpersecond s m labelhindernisabstand zurück. Auf den übrigen m bremst er dann das Auto mit Vollbremsung -- also der bestmöglichen negativen Beschleunigung -- von kilometerperhour auf null ab. Damit finden wir a fracv^s fracleftmeterpersecondright^ m .meterpersecondsquared. So effektiv kann dieses Auto also abbremsen. Wenn es nun mit kilometerperhour in dieselbe Situation kommt so legt es bis der Fahrer anfängt zu Bremsen schon m zurück: s'_textscriptsize R vt meterpersecond s m Bleiben also nur noch m bis zum Hindernis! Die Zeit welche verstreicht bis das Auto am Hindernis ankommt führt auf eine quadratische Gleichung: s fracat^+v_t fracat^ +v_ t -s underbracefrac-.meterpersecondsquared_A t^ underbrace+meterpersecond_B underbracm_C Diese quadratische Gleichung hat die beiden Lösungen t .s t' .s Nur die erste Lösung ist physikalisch sinnvoll. Die Geschwindigkeit welche das Auto am Hindernis noch hat ist somit: v at+v_ -at+v_ labelbremsbeschl -.meterpersecondsquared .s+meterpersecond .meterpersecond approx kilometerperhour Der Wagen trifft also mit einer Geschwindigkeit von rund kilometerperhour auf das Hindernis!
Ein Auto fährt mit kilometerperhour. Plötzlich taucht in m Entfernung ein Hindernis auf und der Fahrer führt eine Vollbremsung durch. Die Reaktionszeit des Fahrers beträgt eine Sekunde d.h. die Zeit verstreicht vom Erkennen des Hindernisses bis zum Einleiten des Bremsvorgangs. Das Auto kommt genau vor dem Hindernis zum Stehen. Nun kommt das gleiche Auto mit kilometerperhour in dieselbe Situation. Mit welcher Gschwin-dig-keit prallt es auf das Hindernis?
Solution:
In der Reaktionszeit die der Fahrer braucht bis er dann auch lich bremst legt er noch eine Strecke von s_textscriptsize R vt labelreaktionsweg meterpersecond s m labelhindernisabstand zurück. Auf den übrigen m bremst er dann das Auto mit Vollbremsung -- also der bestmöglichen negativen Beschleunigung -- von kilometerperhour auf null ab. Damit finden wir a fracv^s fracleftmeterpersecondright^ m .meterpersecondsquared. So effektiv kann dieses Auto also abbremsen. Wenn es nun mit kilometerperhour in dieselbe Situation kommt so legt es bis der Fahrer anfängt zu Bremsen schon m zurück: s'_textscriptsize R vt meterpersecond s m Bleiben also nur noch m bis zum Hindernis! Die Zeit welche verstreicht bis das Auto am Hindernis ankommt führt auf eine quadratische Gleichung: s fracat^+v_t fracat^ +v_ t -s underbracefrac-.meterpersecondsquared_A t^ underbrace+meterpersecond_B underbracm_C Diese quadratische Gleichung hat die beiden Lösungen t .s t' .s Nur die erste Lösung ist physikalisch sinnvoll. Die Geschwindigkeit welche das Auto am Hindernis noch hat ist somit: v at+v_ -at+v_ labelbremsbeschl -.meterpersecondsquared .s+meterpersecond .meterpersecond approx kilometerperhour Der Wagen trifft also mit einer Geschwindigkeit von rund kilometerperhour auf das Hindernis!
Contained in these collections:
-
Beschleunigung Teil 2 by aej
-
Beschleunigung 2 by uz
-
Beschleunigung 2 by aej
-
Beschleunigung II by pw
-
Reaktionszeit by TeXercises

