Rotationsparaboloid
About points...
We associate a certain number of points with each exercise.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
About difficulty...
We associate a certain difficulty with each exercise.
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
Question
Solution
Short
Video
\(\LaTeX\)

No explanation / solution video to this exercise has yet been created.
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Exercise:
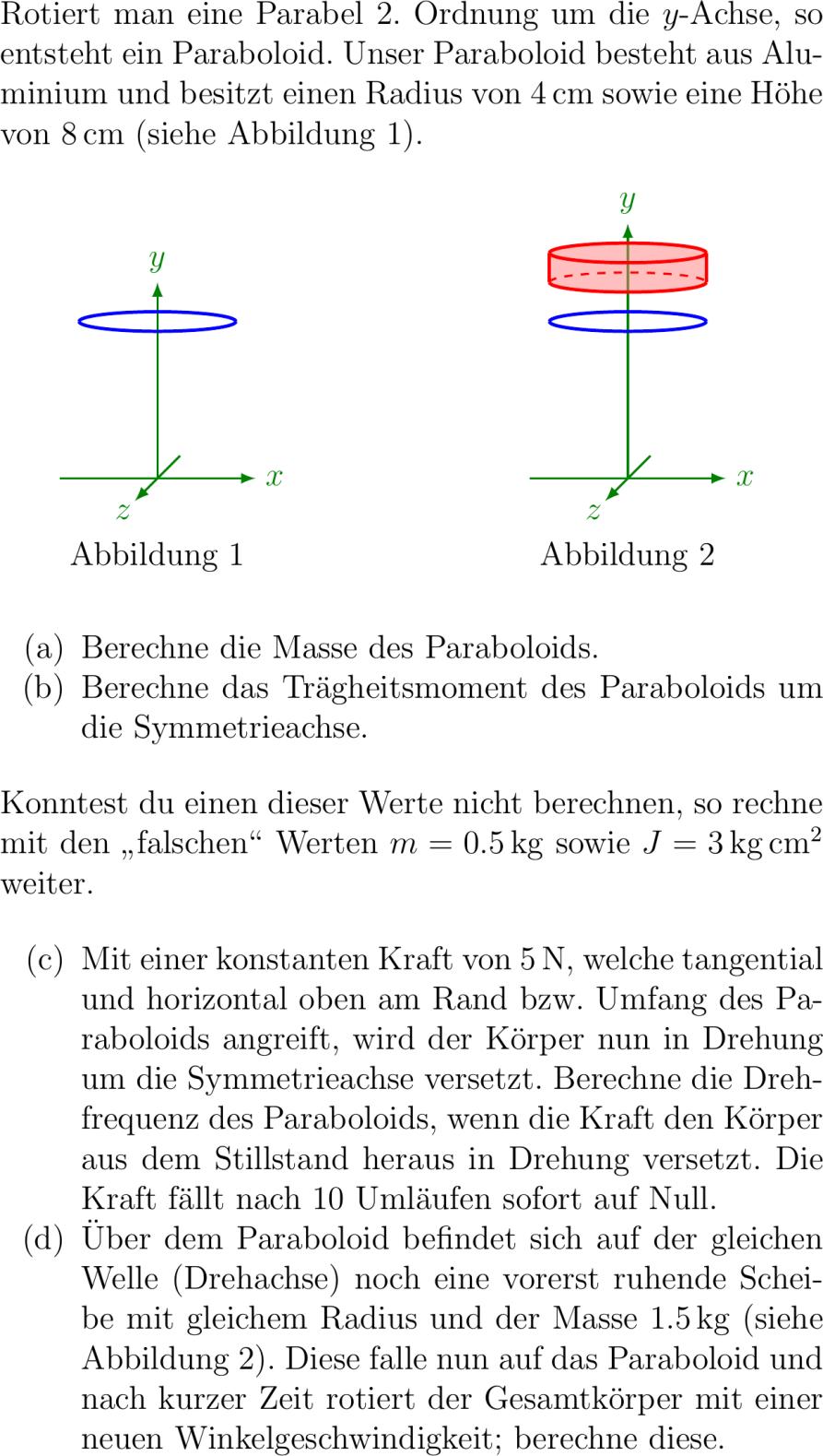
Rotiert man eine Parabel . Ordnung um die y-Achse so entsteht ein Paraboloid. Unser Paraboloid besteht aus Aluminium und besitzt einen Radius von cm sowie eine Höhe von cm siehe Abbildung . center tikzpicturelatex scale. scopelocal bounding boxscope drawthick- colorgreen!!black - -- ; drawthick- colorgreen!!black -- ; drawthick- colorgreen!!black - -- ; filldrawcolorblue fillblue!!white opacity. plotidparaboloid domain-: function.*x*x-- arc ::cm and .cm ; %drawdomain-:variablexblue very thick plot x.x*x; drawcolorblue very thick plotidparaboloid domain-: function.*x*x; drawcolorblue very thick - arc ::cm and .cm; drawcolorblue very thick - arc -::cm and .cm; nodecolorgreen!!black at y; nodecolorgreen!!black at x; nodecolorgreen!!black at . z; node at - Abbildung ; scope scopeshiftcm drawthick- colorgreen!!black - -- ; drawthick- colorgreen!!black -- ; drawthick- colorgreen!!black - -- ; filldrawcolorblue fillblue!!white opacity. plotidparaboloid domain-: function.*x*x-- arc ::cm and .cm ; %drawdomain-:variablexblue very thick plot x.x*x; drawcolorblue very thick plotidparaboloid domain-: function.*x*x; drawcolorblue very thick - arc ::cm and .cm; drawcolorblue very thick - arc -::cm and .cm; filldrawcolorred fillred!!white opacity. - arc -::cm and .cm----.--. arc ::cm and .cm; drawcolorred thick dashed - arc ::cm and .cm; drawcolorred very thick - arc -::cm and .cm; drawcolorred very thick ----.; drawcolorred very thick --.; drawcolorred very thick -. arc ::cm and .cm; drawcolorred very thick -. arc -::cm and .cm; nodecolorgreen!!black at y; nodecolorgreen!!black at x; nodecolorgreen!!black at . z; node at - Abbildung ; scope tikzpicture center enumerate itema Berechne die Masse des Paraboloids. itemb Berechne das Trägheitsmoment des Paraboloids um die Symmetrieachse. enumerate Konntest du einen dieser Werte nicht berechnen so rechne mit den glqq falschengrqq Werten m.kg sowie Jkilogramcentimetersquared weiter. enumerate itemc Mit einer konstanten Kraft von N welche tangential und horizontal oben am Rand bzw. Umfang des Paraboloids angreift wird der Körper nun in Drehung um die Symmetrieachse versetzt. Berechne die Drehfrequenz des Paraboloids wenn die Kraft den Körper aus dem Stillstand heraus in Drehung versetzt. Die Kraft fällt nach Umläufen sofort auf Null. itemd Über dem Paraboloid befindet sich auf der gleichen Welle Drehachse noch eine vorerst ruhe Scheibe mit gleichem Radius und der Masse .kg siehe Abbildung . Diese falle nun auf das Paraboloid und nach kurzer Zeit rotiert der Gesamtkörper mit einer neuen Winkelgeschwindigkeit; berechne diese. enumerate
Solution:
enumerate itema Um die Masse des Paraboloides zu berechnen muss das Volumen bekannt sein. Entweder wird es über einen Ansatz aus der Analysis Rotationskörper oder mittels Zylinderkoordinaten berechnet: m rho mboxdV rho rmboxdrmboxdphimboxdz rho _^pi mboxdphi _^h mboxdz _^sqrtaz rmboxdr rho pi _^h mboxdz leftfrac r^right_^sqrtaz rho pi _^h mboxdz frac az rho pi a leftfrac z^right_^h frac rho pi a h^ rho fracpi a h^ rho fracpi fracr^h h^ pq.kg itemb Das Trägheitsmoment berechnet man wie in Aufgabe a voerteilshaft über Integration in Zylinderkoordinaten: I r^ mboxdm r^ rho mboxdV rho r^ rmboxdrmboxdphimboxdz rho _^pi mboxdphi _^h mboxdz _^sqrtaz r^mboxdr rho pi _^h mboxdz leftfrac r^right_^sqrtaz rho pi _^h mboxdz frac az^ frac rho pi a^ leftfrac z^right_^h frac fracrho pi a h^ rho fracpi ah^ frac ah rho V frac fracr^hh m frac r^ fracmr^ pq.kgm^ itemc Die aufgrund des von der Kraft ausgehen Drehmoments wirke Winkelbeschleunigung ist: alpha fracMI fracrFI pqrad/s^ Die Zeit währ welcher die Kraft wirkt Umdrehungen entsprechen gammapimboxrad ist: t sqrtfracgammaalpha pqs Somit ist die Winkelgeschwindigkeit nach der Krafteinwirkung: omega alpha t pqrad/s quad textund damit f fracomegapi pqHz itemd Wenn die Scheibe auf den rotieren Paraboloiden fällt so gilt Drehimpulserhaltung: L_ L_ I_omega_ I_+I_ omega_ omega_ fracI_omega_I_+I_ pqrad/s^ Dabei wurde verwet dass das Trägheitsmoment der Scheibe I_fracm_r^ ist. enumerate
Rotiert man eine Parabel . Ordnung um die y-Achse so entsteht ein Paraboloid. Unser Paraboloid besteht aus Aluminium und besitzt einen Radius von cm sowie eine Höhe von cm siehe Abbildung . center tikzpicturelatex scale. scopelocal bounding boxscope drawthick- colorgreen!!black - -- ; drawthick- colorgreen!!black -- ; drawthick- colorgreen!!black - -- ; filldrawcolorblue fillblue!!white opacity. plotidparaboloid domain-: function.*x*x-- arc ::cm and .cm ; %drawdomain-:variablexblue very thick plot x.x*x; drawcolorblue very thick plotidparaboloid domain-: function.*x*x; drawcolorblue very thick - arc ::cm and .cm; drawcolorblue very thick - arc -::cm and .cm; nodecolorgreen!!black at y; nodecolorgreen!!black at x; nodecolorgreen!!black at . z; node at - Abbildung ; scope scopeshiftcm drawthick- colorgreen!!black - -- ; drawthick- colorgreen!!black -- ; drawthick- colorgreen!!black - -- ; filldrawcolorblue fillblue!!white opacity. plotidparaboloid domain-: function.*x*x-- arc ::cm and .cm ; %drawdomain-:variablexblue very thick plot x.x*x; drawcolorblue very thick plotidparaboloid domain-: function.*x*x; drawcolorblue very thick - arc ::cm and .cm; drawcolorblue very thick - arc -::cm and .cm; filldrawcolorred fillred!!white opacity. - arc -::cm and .cm----.--. arc ::cm and .cm; drawcolorred thick dashed - arc ::cm and .cm; drawcolorred very thick - arc -::cm and .cm; drawcolorred very thick ----.; drawcolorred very thick --.; drawcolorred very thick -. arc ::cm and .cm; drawcolorred very thick -. arc -::cm and .cm; nodecolorgreen!!black at y; nodecolorgreen!!black at x; nodecolorgreen!!black at . z; node at - Abbildung ; scope tikzpicture center enumerate itema Berechne die Masse des Paraboloids. itemb Berechne das Trägheitsmoment des Paraboloids um die Symmetrieachse. enumerate Konntest du einen dieser Werte nicht berechnen so rechne mit den glqq falschengrqq Werten m.kg sowie Jkilogramcentimetersquared weiter. enumerate itemc Mit einer konstanten Kraft von N welche tangential und horizontal oben am Rand bzw. Umfang des Paraboloids angreift wird der Körper nun in Drehung um die Symmetrieachse versetzt. Berechne die Drehfrequenz des Paraboloids wenn die Kraft den Körper aus dem Stillstand heraus in Drehung versetzt. Die Kraft fällt nach Umläufen sofort auf Null. itemd Über dem Paraboloid befindet sich auf der gleichen Welle Drehachse noch eine vorerst ruhe Scheibe mit gleichem Radius und der Masse .kg siehe Abbildung . Diese falle nun auf das Paraboloid und nach kurzer Zeit rotiert der Gesamtkörper mit einer neuen Winkelgeschwindigkeit; berechne diese. enumerate
Solution:
enumerate itema Um die Masse des Paraboloides zu berechnen muss das Volumen bekannt sein. Entweder wird es über einen Ansatz aus der Analysis Rotationskörper oder mittels Zylinderkoordinaten berechnet: m rho mboxdV rho rmboxdrmboxdphimboxdz rho _^pi mboxdphi _^h mboxdz _^sqrtaz rmboxdr rho pi _^h mboxdz leftfrac r^right_^sqrtaz rho pi _^h mboxdz frac az rho pi a leftfrac z^right_^h frac rho pi a h^ rho fracpi a h^ rho fracpi fracr^h h^ pq.kg itemb Das Trägheitsmoment berechnet man wie in Aufgabe a voerteilshaft über Integration in Zylinderkoordinaten: I r^ mboxdm r^ rho mboxdV rho r^ rmboxdrmboxdphimboxdz rho _^pi mboxdphi _^h mboxdz _^sqrtaz r^mboxdr rho pi _^h mboxdz leftfrac r^right_^sqrtaz rho pi _^h mboxdz frac az^ frac rho pi a^ leftfrac z^right_^h frac fracrho pi a h^ rho fracpi ah^ frac ah rho V frac fracr^hh m frac r^ fracmr^ pq.kgm^ itemc Die aufgrund des von der Kraft ausgehen Drehmoments wirke Winkelbeschleunigung ist: alpha fracMI fracrFI pqrad/s^ Die Zeit währ welcher die Kraft wirkt Umdrehungen entsprechen gammapimboxrad ist: t sqrtfracgammaalpha pqs Somit ist die Winkelgeschwindigkeit nach der Krafteinwirkung: omega alpha t pqrad/s quad textund damit f fracomegapi pqHz itemd Wenn die Scheibe auf den rotieren Paraboloiden fällt so gilt Drehimpulserhaltung: L_ L_ I_omega_ I_+I_ omega_ omega_ fracI_omega_I_+I_ pqrad/s^ Dabei wurde verwet dass das Trägheitsmoment der Scheibe I_fracm_r^ ist. enumerate
Meta Information
Exercise:
Rotiert man eine Parabel . Ordnung um die y-Achse so entsteht ein Paraboloid. Unser Paraboloid besteht aus Aluminium und besitzt einen Radius von cm sowie eine Höhe von cm siehe Abbildung . center tikzpicturelatex scale. scopelocal bounding boxscope drawthick- colorgreen!!black - -- ; drawthick- colorgreen!!black -- ; drawthick- colorgreen!!black - -- ; filldrawcolorblue fillblue!!white opacity. plotidparaboloid domain-: function.*x*x-- arc ::cm and .cm ; %drawdomain-:variablexblue very thick plot x.x*x; drawcolorblue very thick plotidparaboloid domain-: function.*x*x; drawcolorblue very thick - arc ::cm and .cm; drawcolorblue very thick - arc -::cm and .cm; nodecolorgreen!!black at y; nodecolorgreen!!black at x; nodecolorgreen!!black at . z; node at - Abbildung ; scope scopeshiftcm drawthick- colorgreen!!black - -- ; drawthick- colorgreen!!black -- ; drawthick- colorgreen!!black - -- ; filldrawcolorblue fillblue!!white opacity. plotidparaboloid domain-: function.*x*x-- arc ::cm and .cm ; %drawdomain-:variablexblue very thick plot x.x*x; drawcolorblue very thick plotidparaboloid domain-: function.*x*x; drawcolorblue very thick - arc ::cm and .cm; drawcolorblue very thick - arc -::cm and .cm; filldrawcolorred fillred!!white opacity. - arc -::cm and .cm----.--. arc ::cm and .cm; drawcolorred thick dashed - arc ::cm and .cm; drawcolorred very thick - arc -::cm and .cm; drawcolorred very thick ----.; drawcolorred very thick --.; drawcolorred very thick -. arc ::cm and .cm; drawcolorred very thick -. arc -::cm and .cm; nodecolorgreen!!black at y; nodecolorgreen!!black at x; nodecolorgreen!!black at . z; node at - Abbildung ; scope tikzpicture center enumerate itema Berechne die Masse des Paraboloids. itemb Berechne das Trägheitsmoment des Paraboloids um die Symmetrieachse. enumerate Konntest du einen dieser Werte nicht berechnen so rechne mit den glqq falschengrqq Werten m.kg sowie Jkilogramcentimetersquared weiter. enumerate itemc Mit einer konstanten Kraft von N welche tangential und horizontal oben am Rand bzw. Umfang des Paraboloids angreift wird der Körper nun in Drehung um die Symmetrieachse versetzt. Berechne die Drehfrequenz des Paraboloids wenn die Kraft den Körper aus dem Stillstand heraus in Drehung versetzt. Die Kraft fällt nach Umläufen sofort auf Null. itemd Über dem Paraboloid befindet sich auf der gleichen Welle Drehachse noch eine vorerst ruhe Scheibe mit gleichem Radius und der Masse .kg siehe Abbildung . Diese falle nun auf das Paraboloid und nach kurzer Zeit rotiert der Gesamtkörper mit einer neuen Winkelgeschwindigkeit; berechne diese. enumerate
Solution:
enumerate itema Um die Masse des Paraboloides zu berechnen muss das Volumen bekannt sein. Entweder wird es über einen Ansatz aus der Analysis Rotationskörper oder mittels Zylinderkoordinaten berechnet: m rho mboxdV rho rmboxdrmboxdphimboxdz rho _^pi mboxdphi _^h mboxdz _^sqrtaz rmboxdr rho pi _^h mboxdz leftfrac r^right_^sqrtaz rho pi _^h mboxdz frac az rho pi a leftfrac z^right_^h frac rho pi a h^ rho fracpi a h^ rho fracpi fracr^h h^ pq.kg itemb Das Trägheitsmoment berechnet man wie in Aufgabe a voerteilshaft über Integration in Zylinderkoordinaten: I r^ mboxdm r^ rho mboxdV rho r^ rmboxdrmboxdphimboxdz rho _^pi mboxdphi _^h mboxdz _^sqrtaz r^mboxdr rho pi _^h mboxdz leftfrac r^right_^sqrtaz rho pi _^h mboxdz frac az^ frac rho pi a^ leftfrac z^right_^h frac fracrho pi a h^ rho fracpi ah^ frac ah rho V frac fracr^hh m frac r^ fracmr^ pq.kgm^ itemc Die aufgrund des von der Kraft ausgehen Drehmoments wirke Winkelbeschleunigung ist: alpha fracMI fracrFI pqrad/s^ Die Zeit währ welcher die Kraft wirkt Umdrehungen entsprechen gammapimboxrad ist: t sqrtfracgammaalpha pqs Somit ist die Winkelgeschwindigkeit nach der Krafteinwirkung: omega alpha t pqrad/s quad textund damit f fracomegapi pqHz itemd Wenn die Scheibe auf den rotieren Paraboloiden fällt so gilt Drehimpulserhaltung: L_ L_ I_omega_ I_+I_ omega_ omega_ fracI_omega_I_+I_ pqrad/s^ Dabei wurde verwet dass das Trägheitsmoment der Scheibe I_fracm_r^ ist. enumerate
Rotiert man eine Parabel . Ordnung um die y-Achse so entsteht ein Paraboloid. Unser Paraboloid besteht aus Aluminium und besitzt einen Radius von cm sowie eine Höhe von cm siehe Abbildung . center tikzpicturelatex scale. scopelocal bounding boxscope drawthick- colorgreen!!black - -- ; drawthick- colorgreen!!black -- ; drawthick- colorgreen!!black - -- ; filldrawcolorblue fillblue!!white opacity. plotidparaboloid domain-: function.*x*x-- arc ::cm and .cm ; %drawdomain-:variablexblue very thick plot x.x*x; drawcolorblue very thick plotidparaboloid domain-: function.*x*x; drawcolorblue very thick - arc ::cm and .cm; drawcolorblue very thick - arc -::cm and .cm; nodecolorgreen!!black at y; nodecolorgreen!!black at x; nodecolorgreen!!black at . z; node at - Abbildung ; scope scopeshiftcm drawthick- colorgreen!!black - -- ; drawthick- colorgreen!!black -- ; drawthick- colorgreen!!black - -- ; filldrawcolorblue fillblue!!white opacity. plotidparaboloid domain-: function.*x*x-- arc ::cm and .cm ; %drawdomain-:variablexblue very thick plot x.x*x; drawcolorblue very thick plotidparaboloid domain-: function.*x*x; drawcolorblue very thick - arc ::cm and .cm; drawcolorblue very thick - arc -::cm and .cm; filldrawcolorred fillred!!white opacity. - arc -::cm and .cm----.--. arc ::cm and .cm; drawcolorred thick dashed - arc ::cm and .cm; drawcolorred very thick - arc -::cm and .cm; drawcolorred very thick ----.; drawcolorred very thick --.; drawcolorred very thick -. arc ::cm and .cm; drawcolorred very thick -. arc -::cm and .cm; nodecolorgreen!!black at y; nodecolorgreen!!black at x; nodecolorgreen!!black at . z; node at - Abbildung ; scope tikzpicture center enumerate itema Berechne die Masse des Paraboloids. itemb Berechne das Trägheitsmoment des Paraboloids um die Symmetrieachse. enumerate Konntest du einen dieser Werte nicht berechnen so rechne mit den glqq falschengrqq Werten m.kg sowie Jkilogramcentimetersquared weiter. enumerate itemc Mit einer konstanten Kraft von N welche tangential und horizontal oben am Rand bzw. Umfang des Paraboloids angreift wird der Körper nun in Drehung um die Symmetrieachse versetzt. Berechne die Drehfrequenz des Paraboloids wenn die Kraft den Körper aus dem Stillstand heraus in Drehung versetzt. Die Kraft fällt nach Umläufen sofort auf Null. itemd Über dem Paraboloid befindet sich auf der gleichen Welle Drehachse noch eine vorerst ruhe Scheibe mit gleichem Radius und der Masse .kg siehe Abbildung . Diese falle nun auf das Paraboloid und nach kurzer Zeit rotiert der Gesamtkörper mit einer neuen Winkelgeschwindigkeit; berechne diese. enumerate
Solution:
enumerate itema Um die Masse des Paraboloides zu berechnen muss das Volumen bekannt sein. Entweder wird es über einen Ansatz aus der Analysis Rotationskörper oder mittels Zylinderkoordinaten berechnet: m rho mboxdV rho rmboxdrmboxdphimboxdz rho _^pi mboxdphi _^h mboxdz _^sqrtaz rmboxdr rho pi _^h mboxdz leftfrac r^right_^sqrtaz rho pi _^h mboxdz frac az rho pi a leftfrac z^right_^h frac rho pi a h^ rho fracpi a h^ rho fracpi fracr^h h^ pq.kg itemb Das Trägheitsmoment berechnet man wie in Aufgabe a voerteilshaft über Integration in Zylinderkoordinaten: I r^ mboxdm r^ rho mboxdV rho r^ rmboxdrmboxdphimboxdz rho _^pi mboxdphi _^h mboxdz _^sqrtaz r^mboxdr rho pi _^h mboxdz leftfrac r^right_^sqrtaz rho pi _^h mboxdz frac az^ frac rho pi a^ leftfrac z^right_^h frac fracrho pi a h^ rho fracpi ah^ frac ah rho V frac fracr^hh m frac r^ fracmr^ pq.kgm^ itemc Die aufgrund des von der Kraft ausgehen Drehmoments wirke Winkelbeschleunigung ist: alpha fracMI fracrFI pqrad/s^ Die Zeit währ welcher die Kraft wirkt Umdrehungen entsprechen gammapimboxrad ist: t sqrtfracgammaalpha pqs Somit ist die Winkelgeschwindigkeit nach der Krafteinwirkung: omega alpha t pqrad/s quad textund damit f fracomegapi pqHz itemd Wenn die Scheibe auf den rotieren Paraboloiden fällt so gilt Drehimpulserhaltung: L_ L_ I_omega_ I_+I_ omega_ omega_ fracI_omega_I_+I_ pqrad/s^ Dabei wurde verwet dass das Trägheitsmoment der Scheibe I_fracm_r^ ist. enumerate
Contained in these collections:
-
Matura-Training Mechanik by uz
-

