Massenspektrograph
About points...
We associate a certain number of points with each exercise.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
About difficulty...
We associate a certain difficulty with each exercise.
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
Question
Solution
Short
Video
\(\LaTeX\)

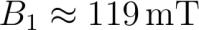
No explanation / solution video to this exercise has yet been created.
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Exercise:
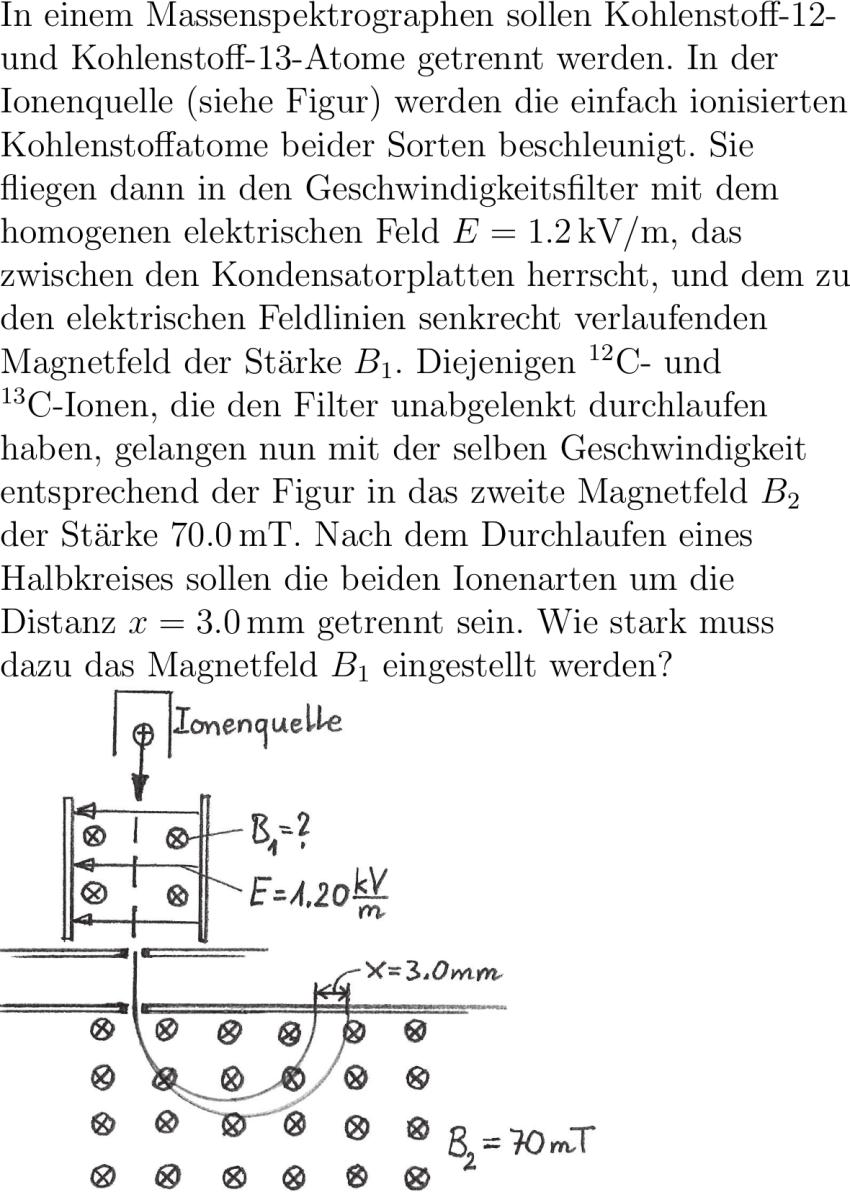
minipagemm raggedright In einem Massenspektrographen sollen Kohlenstoff-- und Kohlenstoff--Atome getrennt werden. In der Ionenquelle siehe Figur werden die einfach ionisierten Kohlenstoffatome beider Sorten beschleunigt. Sie fliegen dann in den Geschwindigkeitsfilter mit dem homogenen elektrischen Feld E .kV/m das zwischen den Kondensatorplatten herrscht und dem zu den elektrischen Feldlinien senkrecht verlaufen Magnetfeld der Stärke B_. Diejenigen ^C- und ^C-Ionen die den Filter unabgelenkt durchlaufen haben gelangen nun mit der selben Geschwindigkeit entsprech der Figur in das zweite Magnetfeld B_ der Stärke .mT. Nach dem Durchlaufen eines Halbkreises sollen die beiden Ionenarten um die Distanz x .mm getrennt sein. Wie stark muss dazu das Magnetfeld B_ eingestellt werden? minipage minipagemmvspacept includegraphicswidthmm#image_path:massenspektrograph# minipage vspaceex
Solution:
Die Lorentzkraft und die elektrische Kraft im Geschwindigkeitsfilter müssen sich gegenseitig aufheben qE qvB_ B_ fracEv.labelmassenspektrograph_ Ausserdem wird die auf die Teilchen wirke Zentripetalkraft durch die Lorentzkraft hervorgerufen m_ fracv^r_ qvB_ r_ fracm_ vqB_. Der gegebene Abstand x der beiden Teilchen bei der Detektion ist x r_-r_quadmboxworaus man r_ r_ + fracx fracm_vqB_ fracm_vqB_ + fracx vfracm_-m_qB_ fracx v fracxqB_m_-m_ erhält. Mit Gleichung refmassenspektrograph_ kann nun v substituiert werden womit man auf B_ fracm_-m_ ExqB_ frac. pq.kg- pq.kgpqm pq.C pq.T pqmT.
minipagemm raggedright In einem Massenspektrographen sollen Kohlenstoff-- und Kohlenstoff--Atome getrennt werden. In der Ionenquelle siehe Figur werden die einfach ionisierten Kohlenstoffatome beider Sorten beschleunigt. Sie fliegen dann in den Geschwindigkeitsfilter mit dem homogenen elektrischen Feld E .kV/m das zwischen den Kondensatorplatten herrscht und dem zu den elektrischen Feldlinien senkrecht verlaufen Magnetfeld der Stärke B_. Diejenigen ^C- und ^C-Ionen die den Filter unabgelenkt durchlaufen haben gelangen nun mit der selben Geschwindigkeit entsprech der Figur in das zweite Magnetfeld B_ der Stärke .mT. Nach dem Durchlaufen eines Halbkreises sollen die beiden Ionenarten um die Distanz x .mm getrennt sein. Wie stark muss dazu das Magnetfeld B_ eingestellt werden? minipage minipagemmvspacept includegraphicswidthmm#image_path:massenspektrograph# minipage vspaceex
Solution:
Die Lorentzkraft und die elektrische Kraft im Geschwindigkeitsfilter müssen sich gegenseitig aufheben qE qvB_ B_ fracEv.labelmassenspektrograph_ Ausserdem wird die auf die Teilchen wirke Zentripetalkraft durch die Lorentzkraft hervorgerufen m_ fracv^r_ qvB_ r_ fracm_ vqB_. Der gegebene Abstand x der beiden Teilchen bei der Detektion ist x r_-r_quadmboxworaus man r_ r_ + fracx fracm_vqB_ fracm_vqB_ + fracx vfracm_-m_qB_ fracx v fracxqB_m_-m_ erhält. Mit Gleichung refmassenspektrograph_ kann nun v substituiert werden womit man auf B_ fracm_-m_ ExqB_ frac. pq.kg- pq.kgpqm pq.C pq.T pqmT.
Meta Information
Exercise:
minipagemm raggedright In einem Massenspektrographen sollen Kohlenstoff-- und Kohlenstoff--Atome getrennt werden. In der Ionenquelle siehe Figur werden die einfach ionisierten Kohlenstoffatome beider Sorten beschleunigt. Sie fliegen dann in den Geschwindigkeitsfilter mit dem homogenen elektrischen Feld E .kV/m das zwischen den Kondensatorplatten herrscht und dem zu den elektrischen Feldlinien senkrecht verlaufen Magnetfeld der Stärke B_. Diejenigen ^C- und ^C-Ionen die den Filter unabgelenkt durchlaufen haben gelangen nun mit der selben Geschwindigkeit entsprech der Figur in das zweite Magnetfeld B_ der Stärke .mT. Nach dem Durchlaufen eines Halbkreises sollen die beiden Ionenarten um die Distanz x .mm getrennt sein. Wie stark muss dazu das Magnetfeld B_ eingestellt werden? minipage minipagemmvspacept includegraphicswidthmm#image_path:massenspektrograph# minipage vspaceex
Solution:
Die Lorentzkraft und die elektrische Kraft im Geschwindigkeitsfilter müssen sich gegenseitig aufheben qE qvB_ B_ fracEv.labelmassenspektrograph_ Ausserdem wird die auf die Teilchen wirke Zentripetalkraft durch die Lorentzkraft hervorgerufen m_ fracv^r_ qvB_ r_ fracm_ vqB_. Der gegebene Abstand x der beiden Teilchen bei der Detektion ist x r_-r_quadmboxworaus man r_ r_ + fracx fracm_vqB_ fracm_vqB_ + fracx vfracm_-m_qB_ fracx v fracxqB_m_-m_ erhält. Mit Gleichung refmassenspektrograph_ kann nun v substituiert werden womit man auf B_ fracm_-m_ ExqB_ frac. pq.kg- pq.kgpqm pq.C pq.T pqmT.
minipagemm raggedright In einem Massenspektrographen sollen Kohlenstoff-- und Kohlenstoff--Atome getrennt werden. In der Ionenquelle siehe Figur werden die einfach ionisierten Kohlenstoffatome beider Sorten beschleunigt. Sie fliegen dann in den Geschwindigkeitsfilter mit dem homogenen elektrischen Feld E .kV/m das zwischen den Kondensatorplatten herrscht und dem zu den elektrischen Feldlinien senkrecht verlaufen Magnetfeld der Stärke B_. Diejenigen ^C- und ^C-Ionen die den Filter unabgelenkt durchlaufen haben gelangen nun mit der selben Geschwindigkeit entsprech der Figur in das zweite Magnetfeld B_ der Stärke .mT. Nach dem Durchlaufen eines Halbkreises sollen die beiden Ionenarten um die Distanz x .mm getrennt sein. Wie stark muss dazu das Magnetfeld B_ eingestellt werden? minipage minipagemmvspacept includegraphicswidthmm#image_path:massenspektrograph# minipage vspaceex
Solution:
Die Lorentzkraft und die elektrische Kraft im Geschwindigkeitsfilter müssen sich gegenseitig aufheben qE qvB_ B_ fracEv.labelmassenspektrograph_ Ausserdem wird die auf die Teilchen wirke Zentripetalkraft durch die Lorentzkraft hervorgerufen m_ fracv^r_ qvB_ r_ fracm_ vqB_. Der gegebene Abstand x der beiden Teilchen bei der Detektion ist x r_-r_quadmboxworaus man r_ r_ + fracx fracm_vqB_ fracm_vqB_ + fracx vfracm_-m_qB_ fracx v fracxqB_m_-m_ erhält. Mit Gleichung refmassenspektrograph_ kann nun v substituiert werden womit man auf B_ fracm_-m_ ExqB_ frac. pq.kg- pq.kgpqm pq.C pq.T pqmT.
Contained in these collections:
-
-
PAM Matura 2009 Stans by uz

