Kupferdrahtspule
About points...
We associate a certain number of points with each exercise.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
About difficulty...
We associate a certain difficulty with each exercise.
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
Question
Solution
Short
Video
\(\LaTeX\)

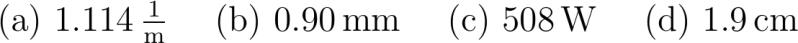
No explanation / solution video to this exercise has yet been created.
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Exercise:
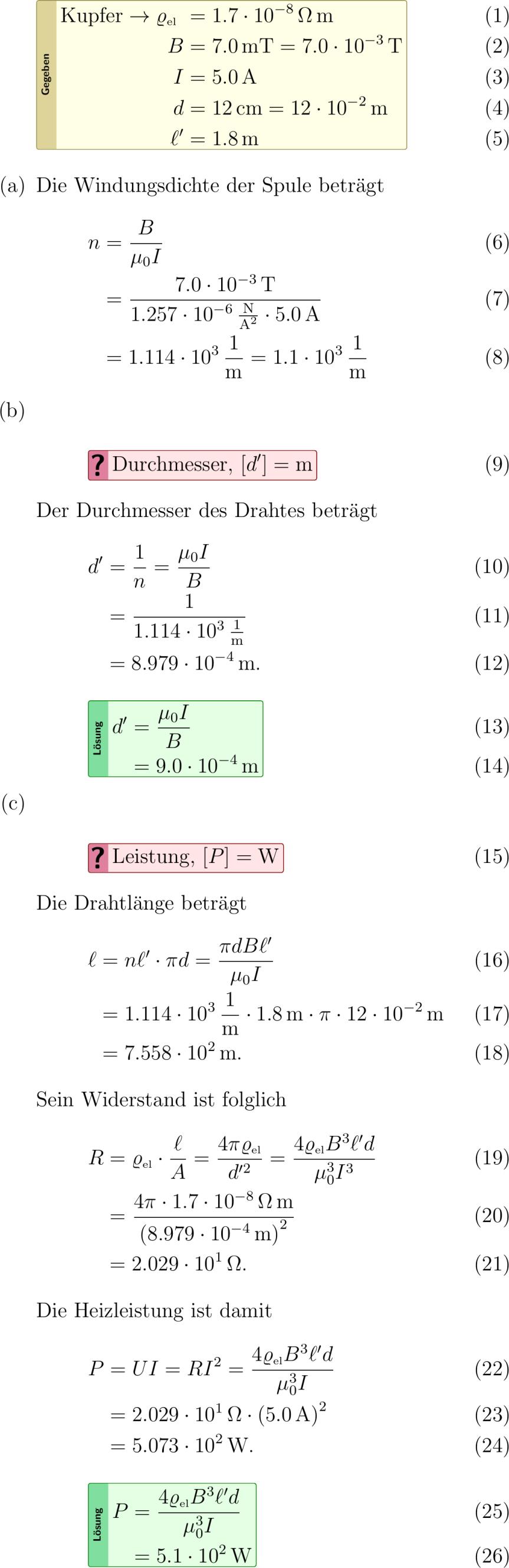
Es sollen die Daten einer Spule aus Kupferdraht Formelbuch.ohmmeter berechnet werden deren magnetische Flussdichte den Wert .mT aufweist. Die Spule werde als lange dünne Spule betrachtet. Sie sei einlagig und dicht gewickelt d.h. nicht mehrere Schichten von Kupferdraht übereinander und Windung liegt an Windung ohne Zwischenraum. abcliste abc Wie muss die Windungsdichte gewählt werden wenn mit einer Stromstärke von .A gearbeitet wird? abc Wie gross muss folglich der Durchmesser des Kupferdrahts sein? Die Dicke der Lackisolation soll vernachlässigt werden. abc Welche Heizleistung entsteht in dieser Spule bei Betrieb wenn die Spule einen Durchmesser von cm und eine Länge von .m aufweist? %abc Wie gross ist der Kurvenradius von Elektronen in dieser Spule wenn die Elektronen mit der Spannung .kV beschleunigt wurden? Der Geschwindigkeitsvektor der Elektronen steht rechtwinklig zum Magnetfeldvektor. abcliste
Solution:
newqtyre.ohmmeter newqtyBo.mT newqtyBBon T newqtyI.A newqtydocm newqtyddon m newqtylp.m newqtymuo.newtonpersquareampere % Geg textKupferpf sscrhoel re B Bo B I I d do d ell' lp abcliste abc Die Windungsdichte der Spule beträgt solqtynfracBmu_IBn/muon*Inpermeter al n nf fracBmuo I n nII abc GesDurchmesserd'sim Der Durchmesser des Drahtes beträgt solqtydprfracmu_IB/nnm al d' fracn dprf fracn dpr. % d' dprf dprII abc GesLeistungP siW Die Drahtlänge beträgt solqtylfracpi d B ell'mu_Inn*lpn*pi*dnm al ell nell' pi d lf n lp pi d l. % Sein Widerstand ist folglich solqtyRfracsscrhoelB^ell'dmu_^I^*ren*ln/dprn**/piohm al R sscrhoel fracellA fracpisscrhoeld'^ Rf fracpi reqtydpr^ R. Die Heizleistung ist damit solqtyPfracsscrhoelB^ell'dmu_^IRn*In**W al P UI RI^ Pf R qtyI^ P. % P Pf PII iffalse abc Die Zentripetalkraft muss gleich gross sein wie die Lorenzkraft d.h. mfracv^r qvB r fracmvqB. Aus der Energiebeziehung qU fracmv^ errechnet man die Geschwindigkeit zu v sqrtfracqUm. Eingesetzt in die Formel für den Radius ergibt sich r fracBsqrtfracmUq ohm.mapprox ohm.cm. fi abcliste
Es sollen die Daten einer Spule aus Kupferdraht Formelbuch.ohmmeter berechnet werden deren magnetische Flussdichte den Wert .mT aufweist. Die Spule werde als lange dünne Spule betrachtet. Sie sei einlagig und dicht gewickelt d.h. nicht mehrere Schichten von Kupferdraht übereinander und Windung liegt an Windung ohne Zwischenraum. abcliste abc Wie muss die Windungsdichte gewählt werden wenn mit einer Stromstärke von .A gearbeitet wird? abc Wie gross muss folglich der Durchmesser des Kupferdrahts sein? Die Dicke der Lackisolation soll vernachlässigt werden. abc Welche Heizleistung entsteht in dieser Spule bei Betrieb wenn die Spule einen Durchmesser von cm und eine Länge von .m aufweist? %abc Wie gross ist der Kurvenradius von Elektronen in dieser Spule wenn die Elektronen mit der Spannung .kV beschleunigt wurden? Der Geschwindigkeitsvektor der Elektronen steht rechtwinklig zum Magnetfeldvektor. abcliste
Solution:
newqtyre.ohmmeter newqtyBo.mT newqtyBBon T newqtyI.A newqtydocm newqtyddon m newqtylp.m newqtymuo.newtonpersquareampere % Geg textKupferpf sscrhoel re B Bo B I I d do d ell' lp abcliste abc Die Windungsdichte der Spule beträgt solqtynfracBmu_IBn/muon*Inpermeter al n nf fracBmuo I n nII abc GesDurchmesserd'sim Der Durchmesser des Drahtes beträgt solqtydprfracmu_IB/nnm al d' fracn dprf fracn dpr. % d' dprf dprII abc GesLeistungP siW Die Drahtlänge beträgt solqtylfracpi d B ell'mu_Inn*lpn*pi*dnm al ell nell' pi d lf n lp pi d l. % Sein Widerstand ist folglich solqtyRfracsscrhoelB^ell'dmu_^I^*ren*ln/dprn**/piohm al R sscrhoel fracellA fracpisscrhoeld'^ Rf fracpi reqtydpr^ R. Die Heizleistung ist damit solqtyPfracsscrhoelB^ell'dmu_^IRn*In**W al P UI RI^ Pf R qtyI^ P. % P Pf PII iffalse abc Die Zentripetalkraft muss gleich gross sein wie die Lorenzkraft d.h. mfracv^r qvB r fracmvqB. Aus der Energiebeziehung qU fracmv^ errechnet man die Geschwindigkeit zu v sqrtfracqUm. Eingesetzt in die Formel für den Radius ergibt sich r fracBsqrtfracmUq ohm.mapprox ohm.cm. fi abcliste
Meta Information
Exercise:
Es sollen die Daten einer Spule aus Kupferdraht Formelbuch.ohmmeter berechnet werden deren magnetische Flussdichte den Wert .mT aufweist. Die Spule werde als lange dünne Spule betrachtet. Sie sei einlagig und dicht gewickelt d.h. nicht mehrere Schichten von Kupferdraht übereinander und Windung liegt an Windung ohne Zwischenraum. abcliste abc Wie muss die Windungsdichte gewählt werden wenn mit einer Stromstärke von .A gearbeitet wird? abc Wie gross muss folglich der Durchmesser des Kupferdrahts sein? Die Dicke der Lackisolation soll vernachlässigt werden. abc Welche Heizleistung entsteht in dieser Spule bei Betrieb wenn die Spule einen Durchmesser von cm und eine Länge von .m aufweist? %abc Wie gross ist der Kurvenradius von Elektronen in dieser Spule wenn die Elektronen mit der Spannung .kV beschleunigt wurden? Der Geschwindigkeitsvektor der Elektronen steht rechtwinklig zum Magnetfeldvektor. abcliste
Solution:
newqtyre.ohmmeter newqtyBo.mT newqtyBBon T newqtyI.A newqtydocm newqtyddon m newqtylp.m newqtymuo.newtonpersquareampere % Geg textKupferpf sscrhoel re B Bo B I I d do d ell' lp abcliste abc Die Windungsdichte der Spule beträgt solqtynfracBmu_IBn/muon*Inpermeter al n nf fracBmuo I n nII abc GesDurchmesserd'sim Der Durchmesser des Drahtes beträgt solqtydprfracmu_IB/nnm al d' fracn dprf fracn dpr. % d' dprf dprII abc GesLeistungP siW Die Drahtlänge beträgt solqtylfracpi d B ell'mu_Inn*lpn*pi*dnm al ell nell' pi d lf n lp pi d l. % Sein Widerstand ist folglich solqtyRfracsscrhoelB^ell'dmu_^I^*ren*ln/dprn**/piohm al R sscrhoel fracellA fracpisscrhoeld'^ Rf fracpi reqtydpr^ R. Die Heizleistung ist damit solqtyPfracsscrhoelB^ell'dmu_^IRn*In**W al P UI RI^ Pf R qtyI^ P. % P Pf PII iffalse abc Die Zentripetalkraft muss gleich gross sein wie die Lorenzkraft d.h. mfracv^r qvB r fracmvqB. Aus der Energiebeziehung qU fracmv^ errechnet man die Geschwindigkeit zu v sqrtfracqUm. Eingesetzt in die Formel für den Radius ergibt sich r fracBsqrtfracmUq ohm.mapprox ohm.cm. fi abcliste
Es sollen die Daten einer Spule aus Kupferdraht Formelbuch.ohmmeter berechnet werden deren magnetische Flussdichte den Wert .mT aufweist. Die Spule werde als lange dünne Spule betrachtet. Sie sei einlagig und dicht gewickelt d.h. nicht mehrere Schichten von Kupferdraht übereinander und Windung liegt an Windung ohne Zwischenraum. abcliste abc Wie muss die Windungsdichte gewählt werden wenn mit einer Stromstärke von .A gearbeitet wird? abc Wie gross muss folglich der Durchmesser des Kupferdrahts sein? Die Dicke der Lackisolation soll vernachlässigt werden. abc Welche Heizleistung entsteht in dieser Spule bei Betrieb wenn die Spule einen Durchmesser von cm und eine Länge von .m aufweist? %abc Wie gross ist der Kurvenradius von Elektronen in dieser Spule wenn die Elektronen mit der Spannung .kV beschleunigt wurden? Der Geschwindigkeitsvektor der Elektronen steht rechtwinklig zum Magnetfeldvektor. abcliste
Solution:
newqtyre.ohmmeter newqtyBo.mT newqtyBBon T newqtyI.A newqtydocm newqtyddon m newqtylp.m newqtymuo.newtonpersquareampere % Geg textKupferpf sscrhoel re B Bo B I I d do d ell' lp abcliste abc Die Windungsdichte der Spule beträgt solqtynfracBmu_IBn/muon*Inpermeter al n nf fracBmuo I n nII abc GesDurchmesserd'sim Der Durchmesser des Drahtes beträgt solqtydprfracmu_IB/nnm al d' fracn dprf fracn dpr. % d' dprf dprII abc GesLeistungP siW Die Drahtlänge beträgt solqtylfracpi d B ell'mu_Inn*lpn*pi*dnm al ell nell' pi d lf n lp pi d l. % Sein Widerstand ist folglich solqtyRfracsscrhoelB^ell'dmu_^I^*ren*ln/dprn**/piohm al R sscrhoel fracellA fracpisscrhoeld'^ Rf fracpi reqtydpr^ R. Die Heizleistung ist damit solqtyPfracsscrhoelB^ell'dmu_^IRn*In**W al P UI RI^ Pf R qtyI^ P. % P Pf PII iffalse abc Die Zentripetalkraft muss gleich gross sein wie die Lorenzkraft d.h. mfracv^r qvB r fracmvqB. Aus der Energiebeziehung qU fracmv^ errechnet man die Geschwindigkeit zu v sqrtfracqUm. Eingesetzt in die Formel für den Radius ergibt sich r fracBsqrtfracmUq ohm.mapprox ohm.cm. fi abcliste
Contained in these collections:
-
-
-
PAM Matura 2008 Stans by uz

